
Question Number 140270 by liberty last updated on 06/May/21
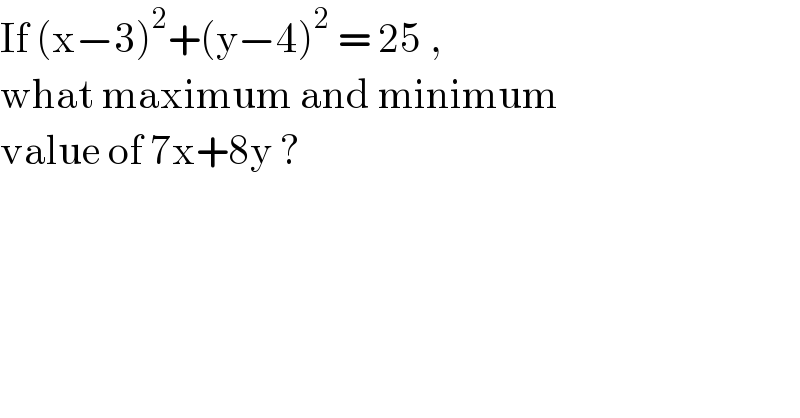
$$\mathrm{If}\:\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{4}\right)^{\mathrm{2}} \:=\:\mathrm{25}\:, \\ $$$$\mathrm{what}\:\mathrm{maximum}\:\mathrm{and}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{7x}+\mathrm{8y}\:? \\ $$
Answered by EDWIN88 last updated on 06/May/21
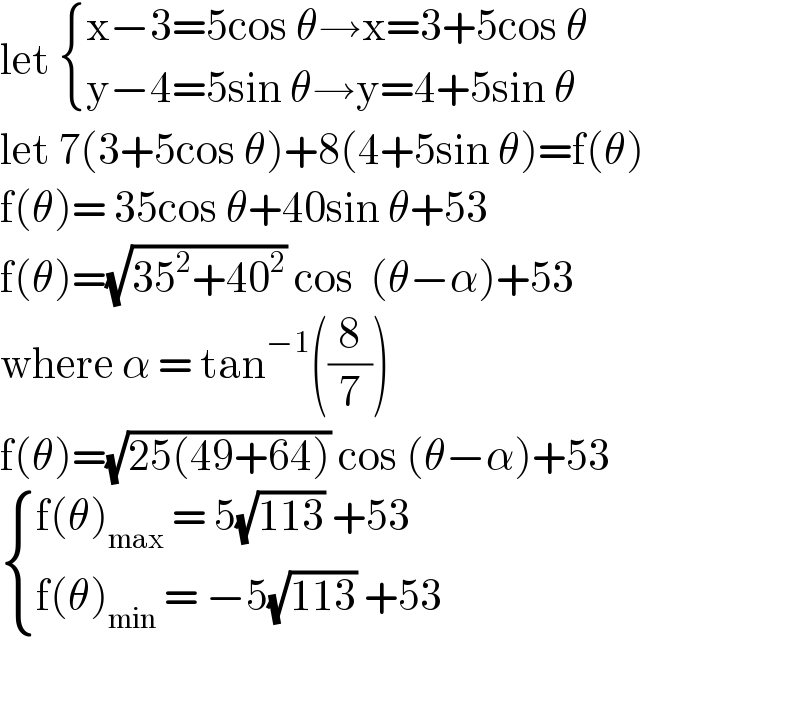
$$\mathrm{let}\:\begin{cases}{\mathrm{x}−\mathrm{3}=\mathrm{5cos}\:\theta\rightarrow\mathrm{x}=\mathrm{3}+\mathrm{5cos}\:\theta}\\{\mathrm{y}−\mathrm{4}=\mathrm{5sin}\:\theta\rightarrow\mathrm{y}=\mathrm{4}+\mathrm{5sin}\:\theta}\end{cases} \\ $$$$\mathrm{let}\:\mathrm{7}\left(\mathrm{3}+\mathrm{5cos}\:\theta\right)+\mathrm{8}\left(\mathrm{4}+\mathrm{5sin}\:\theta\right)=\mathrm{f}\left(\theta\right) \\ $$$$\mathrm{f}\left(\theta\right)=\:\mathrm{35cos}\:\theta+\mathrm{40sin}\:\theta+\mathrm{53} \\ $$$$\mathrm{f}\left(\theta\right)=\sqrt{\mathrm{35}^{\mathrm{2}} +\mathrm{40}^{\mathrm{2}} }\:\mathrm{cos}\:\:\left(\theta−\alpha\right)+\mathrm{53} \\ $$$$\mathrm{where}\:\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{8}}{\mathrm{7}}\right) \\ $$$$\mathrm{f}\left(\theta\right)=\sqrt{\mathrm{25}\left(\mathrm{49}+\mathrm{64}\right)}\:\mathrm{cos}\:\left(\theta−\alpha\right)+\mathrm{53} \\ $$$$\begin{cases}{\mathrm{f}\left(\theta\right)_{\mathrm{max}} \:=\:\mathrm{5}\sqrt{\mathrm{113}}\:+\mathrm{53}}\\{\mathrm{f}\left(\theta\right)_{\mathrm{min}} \:=\:−\mathrm{5}\sqrt{\mathrm{113}}\:+\mathrm{53}\:}\end{cases} \\ $$$$ \\ $$
Answered by mr W last updated on 06/May/21
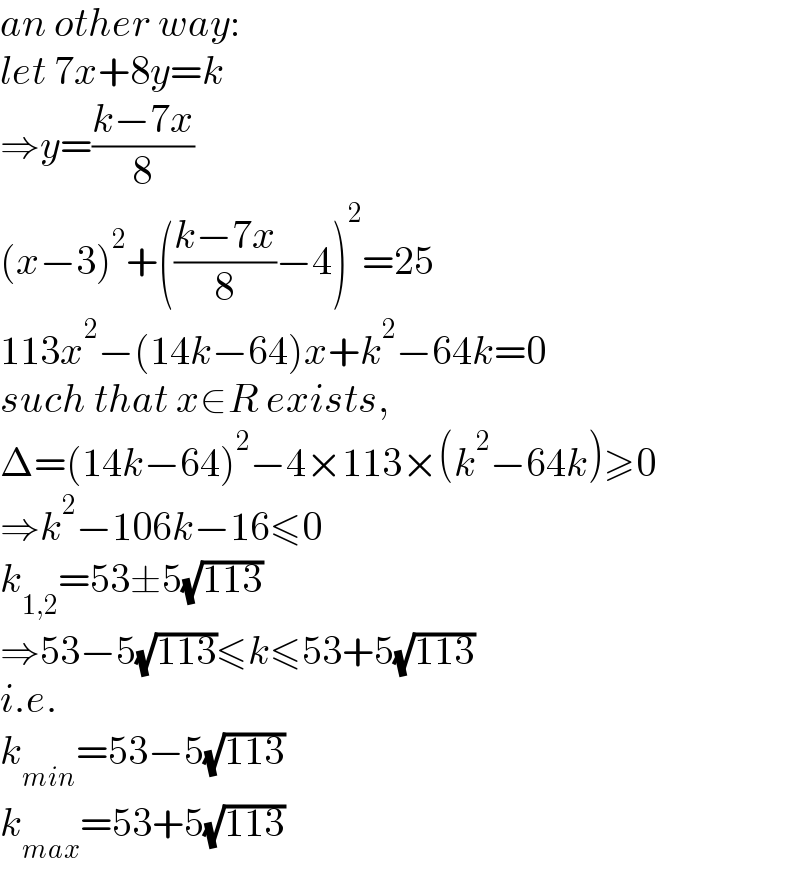
$${an}\:{other}\:{way}: \\ $$$${let}\:\mathrm{7}{x}+\mathrm{8}{y}={k} \\ $$$$\Rightarrow{y}=\frac{{k}−\mathrm{7}{x}}{\mathrm{8}} \\ $$$$\left({x}−\mathrm{3}\right)^{\mathrm{2}} +\left(\frac{{k}−\mathrm{7}{x}}{\mathrm{8}}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\mathrm{113}{x}^{\mathrm{2}} −\left(\mathrm{14}{k}−\mathrm{64}\right){x}+{k}^{\mathrm{2}} −\mathrm{64}{k}=\mathrm{0} \\ $$$${such}\:{that}\:{x}\in{R}\:{exists}, \\ $$$$\Delta=\left(\mathrm{14}{k}−\mathrm{64}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{113}×\left({k}^{\mathrm{2}} −\mathrm{64}{k}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{k}^{\mathrm{2}} −\mathrm{106}{k}−\mathrm{16}\leqslant\mathrm{0} \\ $$$${k}_{\mathrm{1},\mathrm{2}} =\mathrm{53}\pm\mathrm{5}\sqrt{\mathrm{113}} \\ $$$$\Rightarrow\mathrm{53}−\mathrm{5}\sqrt{\mathrm{113}}\leqslant{k}\leqslant\mathrm{53}+\mathrm{5}\sqrt{\mathrm{113}} \\ $$$${i}.{e}. \\ $$$${k}_{{min}} =\mathrm{53}−\mathrm{5}\sqrt{\mathrm{113}} \\ $$$${k}_{{max}} =\mathrm{53}+\mathrm{5}\sqrt{\mathrm{113}} \\ $$
