
Question Number 171371 by pticantor last updated on 13/Jun/22
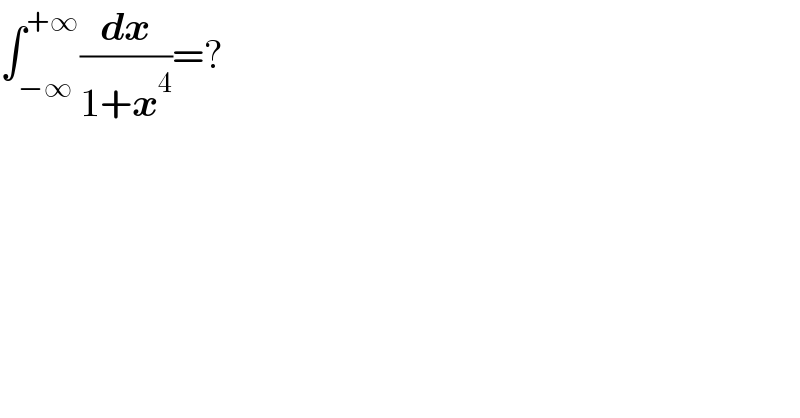
$$\int_{−\infty} ^{+\infty} \frac{\boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{4}} }=? \\ $$
Answered by aleks041103 last updated on 13/Jun/22
![solve using complex analysis we inregrate the complex function (1/(1+z^4 )) over the contour Γ=lim_(r→∞) Γ_1 ∪Γ_2 . Γ_1 :=[−r,r] and Γ_2 :={re^(it) ∣t∈(0,π)} ⇒I=∮_Γ (dz/(1+z^4 ))=∫_Γ_1 (dz/(1+z^4 ))+∫_Γ_2 (dz/(1+z^4 )) ∫_Γ_1 (dz/(1+z^4 ))=∫_(−∞) ^(+∞) (dx/(1+x^4 )) ∫_Γ_2 (dz/(1+z^4 ))=lim_(r→∞) ∫_0 ^π ((ire^(it) dt)/(1+r^4 e^(4it) ))= =lim_(r→∞) ((ir)/r^4 )∫_0 ^π e^(−3it) dt=0 ⇒Ans.=∮_Γ (dz/(1+z^4 ))=2πiΣRes(z_i ) 1+z^4 =0 z^4 =e^(iπ) =e^(i(π+2kπ)) ⇒z=e^(i((π/4)+((kπ)/2))) therefore we have z_1 =e^(iπ/4) =(1/( (√2)))+(i/( (√2))),Im(z_1 )>0 z_2 =e^(3iπ/4) =−(1/( (√2)))+(i/( (√2))),Im(z_2 )>0 z_3 =e^(5iπ/4) =−(1/( (√2)))−(i/( (√2))),Im(z_3 )<0 z_4 =e^(7iπ/4) =(1/( (√2)))−(i/( (√2))),Im(z_4 )<0 1+z^4 =(z−z_1 )(z−z_2 )(z−z_3 )(z−z_4 ) ⇒we have poles of (1/(1+z^4 )) in bounds of Γ at z_1 and z_2 and those poles are simple. ⇒Res(z_1 )=lim_(z→z_1 ) ((z−z_1 )/(1+z^4 ))=(1/(4z_1 ^3 ))=(1/4) (z_1 /z_1 ^4 )=−(1/4)e^(iπ/4) Res(z_2 )=lim_(z→z_2 ) ((z−z_2 )/(1+z^4 ))=(1/(4z_2 ^3 ))=(1/4) (z_2 /z_2 ^4 )=−(1/4)ie^(iπ/2) ΣRes(z_i )=−(1/4)(1+i)e^(iπ/4) = =−((√2)/4)((1/( (√2)))+(i/( (√2))))e^(iπ/4) = =−((√2)/4)e^(iπ/2) =−(i/(2(√2))) ⇒∫_(−∞) ^(+∞) (dx/(1+x^4 ))=2πi(−(i/(2(√2))))=(π/( (√2)))](Q171373.png)
$${solve}\:{using}\:{complex}\:{analysis} \\ $$$${we}\:{inregrate}\:{the}\:{complex}\:{function} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{4}} }\:{over}\:{the}\:{contour}\:\Gamma=\underset{{r}\rightarrow\infty} {{lim}}\Gamma_{\mathrm{1}} \cup\Gamma_{\mathrm{2}} . \\ $$$$\Gamma_{\mathrm{1}} :=\left[−{r},{r}\right]\:{and}\:\Gamma_{\mathrm{2}} :=\left\{{re}^{{it}} \mid{t}\in\left(\mathrm{0},\pi\right)\right\} \\ $$$$\Rightarrow{I}=\oint_{\Gamma} \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }=\int_{\Gamma_{\mathrm{1}} } \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }+\int_{\Gamma_{\mathrm{2}} } \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{4}} } \\ $$$$\int_{\Gamma_{\mathrm{1}} } \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }=\int_{−\infty} ^{+\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} } \\ $$$$\int_{\Gamma_{\mathrm{2}} } \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }=\underset{{r}\rightarrow\infty} {{lim}}\int_{\mathrm{0}} ^{\pi} \frac{{ire}^{{it}} {dt}}{\mathrm{1}+{r}^{\mathrm{4}} {e}^{\mathrm{4}{it}} }= \\ $$$$=\underset{{r}\rightarrow\infty} {{lim}}\frac{{ir}}{{r}^{\mathrm{4}} }\int_{\mathrm{0}} ^{\pi} {e}^{−\mathrm{3}{it}} {dt}=\mathrm{0} \\ $$$$\Rightarrow{Ans}.=\oint_{\Gamma} \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }=\mathrm{2}\pi{i}\Sigma{Res}\left({z}_{{i}} \right) \\ $$$$\mathrm{1}+{z}^{\mathrm{4}} =\mathrm{0} \\ $$$${z}^{\mathrm{4}} ={e}^{{i}\pi} ={e}^{{i}\left(\pi+\mathrm{2}{k}\pi\right)} \Rightarrow{z}={e}^{{i}\left(\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{2}}\right)} \\ $$$${therefore}\:{we}\:{have} \\ $$$${z}_{\mathrm{1}} ={e}^{{i}\pi/\mathrm{4}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{{i}}{\:\sqrt{\mathrm{2}}},{Im}\left({z}_{\mathrm{1}} \right)>\mathrm{0} \\ $$$${z}_{\mathrm{2}} ={e}^{\mathrm{3}{i}\pi/\mathrm{4}} =−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{{i}}{\:\sqrt{\mathrm{2}}},{Im}\left({z}_{\mathrm{2}} \right)>\mathrm{0} \\ $$$${z}_{\mathrm{3}} ={e}^{\mathrm{5}{i}\pi/\mathrm{4}} =−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}},{Im}\left({z}_{\mathrm{3}} \right)<\mathrm{0} \\ $$$${z}_{\mathrm{4}} ={e}^{\mathrm{7}{i}\pi/\mathrm{4}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}},{Im}\left({z}_{\mathrm{4}} \right)<\mathrm{0} \\ $$$$\mathrm{1}+{z}^{\mathrm{4}} =\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)\left({z}−{z}_{\mathrm{3}} \right)\left({z}−{z}_{\mathrm{4}} \right) \\ $$$$\Rightarrow{we}\:{have}\:{poles}\:{of}\:\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{4}} }\:{in}\:{bounds} \\ $$$${of}\:\Gamma\:{at}\:{z}_{\mathrm{1}} \:{and}\:{z}_{\mathrm{2}} \:{and}\:{those}\:{poles}\:{are} \\ $$$${simple}. \\ $$$$\Rightarrow{Res}\left({z}_{\mathrm{1}} \right)=\underset{{z}\rightarrow{z}_{\mathrm{1}} } {{lim}}\frac{{z}−{z}_{\mathrm{1}} }{\mathrm{1}+{z}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{4}{z}_{\mathrm{1}} ^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{1}} ^{\mathrm{4}} }=−\frac{\mathrm{1}}{\mathrm{4}}{e}^{{i}\pi/\mathrm{4}} \\ $$$${Res}\left({z}_{\mathrm{2}} \right)=\underset{{z}\rightarrow{z}_{\mathrm{2}} } {{lim}}\frac{{z}−{z}_{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{4}{z}_{\mathrm{2}} ^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{z}_{\mathrm{2}} }{{z}_{\mathrm{2}} ^{\mathrm{4}} }=−\frac{\mathrm{1}}{\mathrm{4}}{ie}^{{i}\pi/\mathrm{2}} \\ $$$$\Sigma{Res}\left({z}_{{i}} \right)=−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+{i}\right){e}^{{i}\pi/\mathrm{4}} = \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right){e}^{{i}\pi/\mathrm{4}} = \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}{e}^{{i}\pi/\mathrm{2}} =−\frac{{i}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }=\mathrm{2}\pi{i}\left(−\frac{{i}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Answered by Mathspace last updated on 14/Jun/22
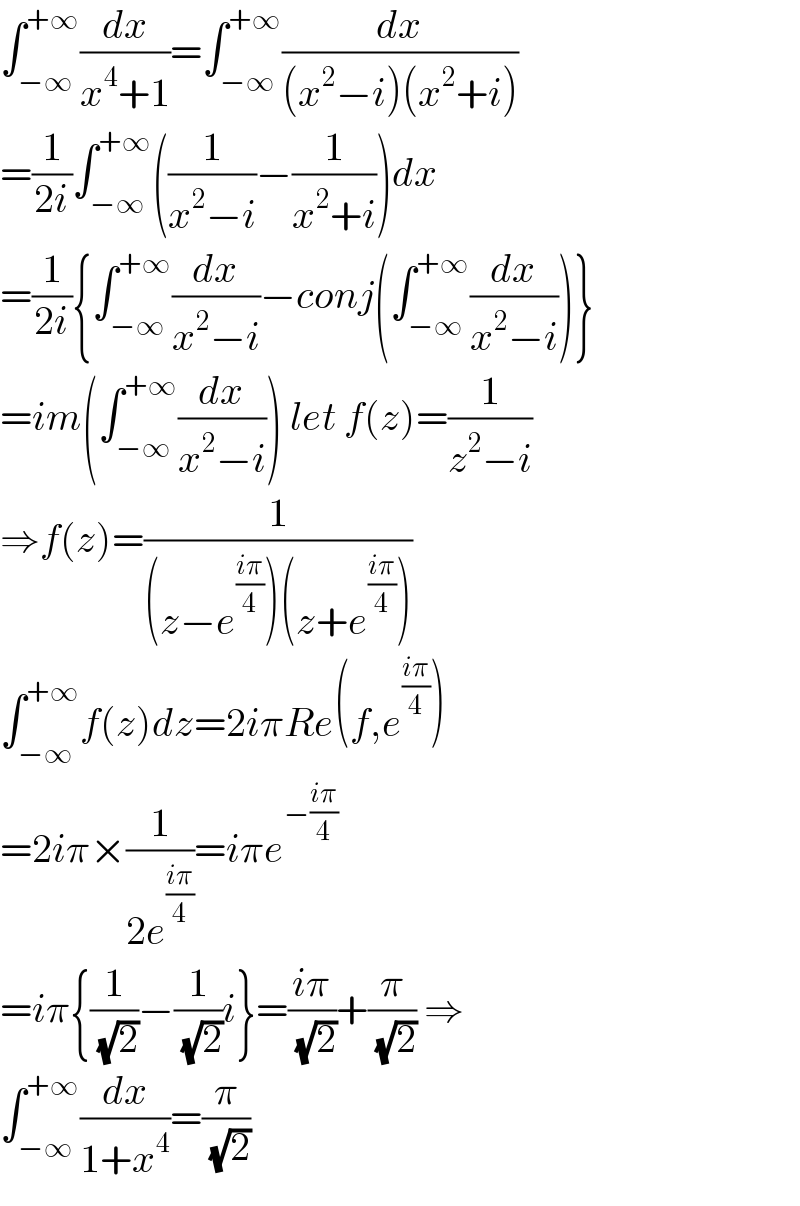
$$\int_{−\infty} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{1}}=\int_{−\infty} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} −{i}\right)\left({x}^{\mathrm{2}} +{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\int_{−\infty} ^{+\infty} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{i}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{i}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\int_{−\infty} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{2}} −{i}}−{conj}\left(\int_{−\infty} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{2}} −{i}}\right)\right\} \\ $$$$={im}\left(\int_{−\infty} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{2}} −{i}}\right)\:{let}\:{f}\left({z}\right)=\frac{\mathrm{1}}{{z}^{\mathrm{2}} −{i}} \\ $$$$\Rightarrow{f}\left({z}\right)=\frac{\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} {f}\left({z}\right){dz}=\mathrm{2}{i}\pi{Re}\left({f},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right) \\ $$$$=\mathrm{2}{i}\pi×\frac{\mathrm{1}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} }={i}\pi{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$$={i}\pi\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right\}=\frac{{i}\pi}{\:\sqrt{\mathrm{2}}}+\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Answered by floor(10²Eta[1]) last updated on 14/Jun/22
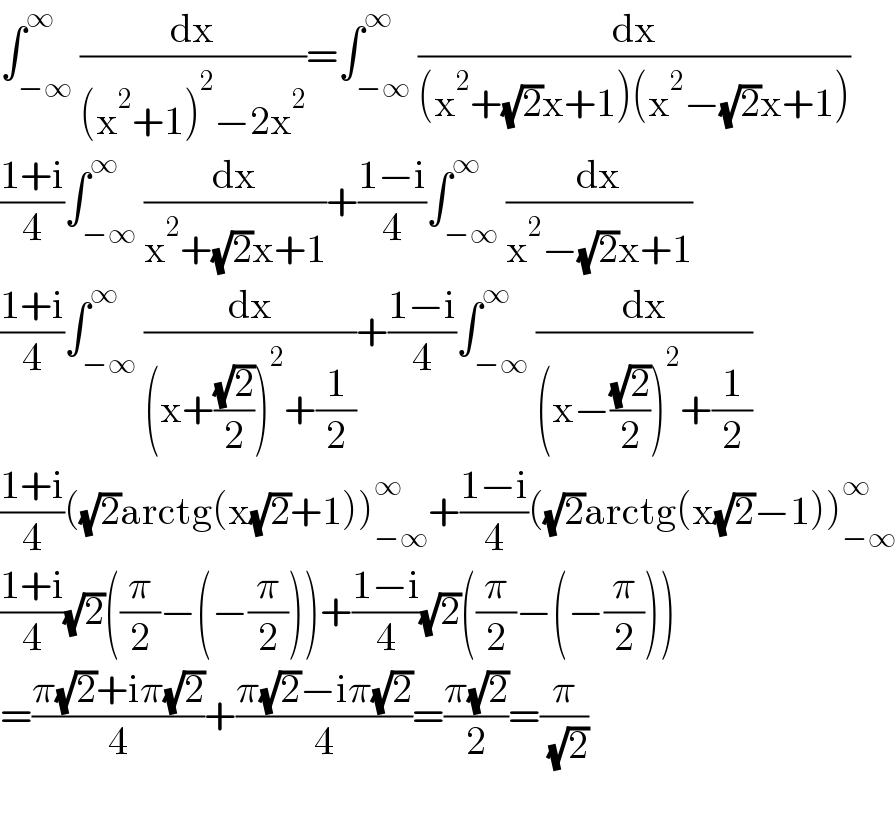
$$\int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2x}^{\mathrm{2}} }=\int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}+\mathrm{i}}{\mathrm{4}}\int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{4}}\int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{x}+\mathrm{1}} \\ $$$$\frac{\mathrm{1}+\mathrm{i}}{\mathrm{4}}\int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{4}}\int_{−\infty} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}+\mathrm{i}}{\mathrm{4}}\left(\sqrt{\mathrm{2}}\mathrm{arctg}\left(\mathrm{x}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right)_{−\infty} ^{\infty} +\frac{\mathrm{1}−\mathrm{i}}{\mathrm{4}}\left(\sqrt{\mathrm{2}}\mathrm{arctg}\left(\mathrm{x}\sqrt{\mathrm{2}}−\mathrm{1}\right)\right)_{−\infty} ^{\infty} \\ $$$$\frac{\mathrm{1}+\mathrm{i}}{\mathrm{4}}\sqrt{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right)+\frac{\mathrm{1}−\mathrm{i}}{\mathrm{4}}\sqrt{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\left(−\frac{\pi}{\mathrm{2}}\right)\right) \\ $$$$=\frac{\pi\sqrt{\mathrm{2}}+\mathrm{i}\pi\sqrt{\mathrm{2}}}{\mathrm{4}}+\frac{\pi\sqrt{\mathrm{2}}−\mathrm{i}\pi\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$
