Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140601 by mathdanisur last updated on 10/May/21

∫_0 ^∞ ((log(1+z^4 ))/( (√z)(1+z)))dz

$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{log}\left(\mathrm{1}+{z}^{\mathrm{4}} \right)}{\:\sqrt{{z}}\left(\mathrm{1}+{z}\right)}{dz} \\ $$

Answered by mathmax by abdo last updated on 10/May/21

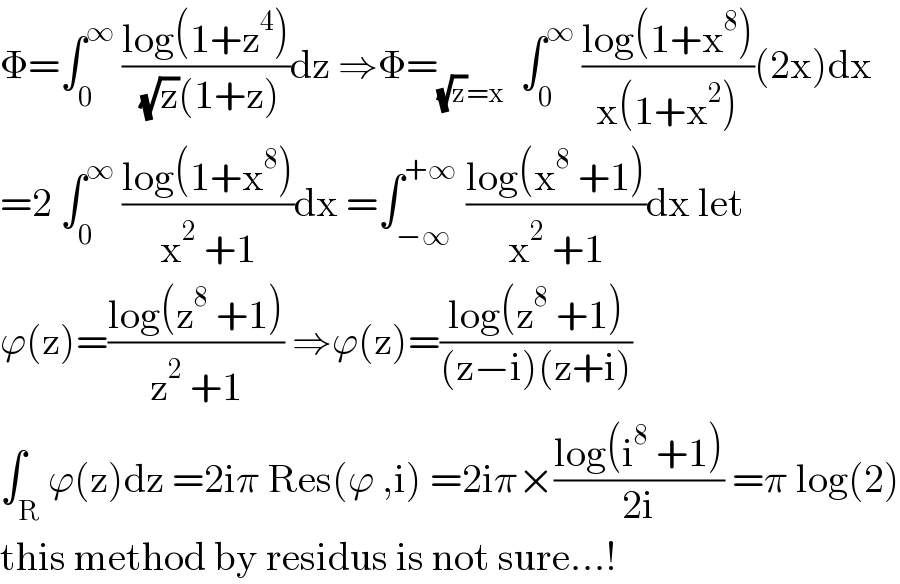
Φ=∫_0 ^∞ ((log(1+z^4 ))/( (√z)(1+z)))dz ⇒Φ=_((√z)=x) ∫_0 ^∞ ((log(1+x^8 ))/(x(1+x^2 )))(2x)dx =2 ∫_0 ^∞ ((log(1+x^8 ))/(x^2 +1))dx =∫_(−∞) ^(+∞) ((log(x^8 +1))/(x^2 +1))dx let ϕ(z)=((log(z^8 +1))/(z^2 +1)) ⇒ϕ(z)=((log(z^8 +1))/((z−i)(z+i))) ∫_R ϕ(z)dz =2iπ Res(ϕ ,i) =2iπ×((log(i^8 +1))/(2i)) =π log(2) this method by residus is not sure...!

$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{z}^{\mathrm{4}} \right)}{\:\sqrt{\mathrm{z}}\left(\mathrm{1}+\mathrm{z}\right)}\mathrm{dz}\:\Rightarrow\Phi=_{\sqrt{\mathrm{z}}=\mathrm{x}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{8}} \right)}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}^{\mathrm{8}} \right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{log}\left(\mathrm{x}^{\mathrm{8}} \:+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\mathrm{let} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{log}\left(\mathrm{z}^{\mathrm{8}} \:+\mathrm{1}\right)}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{log}\left(\mathrm{z}^{\mathrm{8}} \:+\mathrm{1}\right)}{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)} \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi\:,\mathrm{i}\right)\:=\mathrm{2i}\pi×\frac{\mathrm{log}\left(\mathrm{i}^{\mathrm{8}} \:+\mathrm{1}\right)}{\mathrm{2i}}\:=\pi\:\mathrm{log}\left(\mathrm{2}\right) \\ $$$$\mathrm{this}\:\mathrm{method}\:\mathrm{by}\:\mathrm{residus}\:\mathrm{is}\:\mathrm{not}\:\mathrm{sure}...! \\ $$

Commented by mathmax by abdo last updated on 10/May/21

let try another way Φ=2 ∫_0 ^∞ ((log(x^8 +1))/(x^2 +1))dx =∫_(−∞) ^(+∞) ((log(x^8 +1))/(x^2 +1))dx let f(a) =∫_(−∞) ^(+∞) ((log(x^8 +a^8 ))/(x^2 +1))dx we have f(1)=Φ f^′ (a)=∫_(−∞) ^(+∞) ((8a^7 )/((x^8 +a^8 )(x^2 +1)))dx =8a^7 ∫_(−∞) ^(+∞) (dx/((x^8 +a^8 )(x^2 +1))) x^8 +a^8 =0 ⇒((x/a))^8 =−1 =e^((2k+1)iπ) ⇒x^8 =a^8 e^((2k+1)iπ) ⇒ x_k =a e^(i(2k+1)(π/8)) ⇒x^8 +a^8 =Π_(k=0) ^7 (x−a e^(i(2k+1)(π/8)) ) let ϕ(z)=(1/((z^8 +a^8 )(z^2 +1))) ⇒ϕ(z)=(1/((z−i)(z+i)Π_(k=0) ^7 (z−ae^(i(2k+1)(π/8)) ))) z_k =ae^((i(2k+1)π)/8) ⇒z_0 =a e^((iπ)/8) ,z_1 =ae^(i((3π)/8)) ,z_2 =ae^((i5π)/8) z_3 =a e^((i7π)/8) ,z_4 =ae^((i9π)/8) ,z_5 =ae^((i11π)/8) ,z_6 =ae^((i13π)/8) ,z_7 =ae^((i15π)/8) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,i)+Res(ϕ ,ae^((iπ)/8) )+Res(ϕ,ae^((i3π)/8) ) +Res(ϕ,a e^((i5π)/8) )} Res(ϕ,i)=(1/(2iΠ_(k=0) ^7 (i−ae^(i(2k+1)(π/8)) ))) ϕ(z)=(1/(z^(10) +z^8 +a^8 z^2 +a^8 ))=(1/(p(z))) ⇒Res(ϕ ,z_i ) =(1/(p^′ (z_i ))) =(1/(10z_i ^9 +8 z_i ^7 +2a^8 z_i )) ⇒ Res(ϕ,ae^((iπ)/8) ) =(1/(10(ae^((iπ)/8) )^9 +8(ae^((iπ)/8) )^7 +2a^8 (ae^((iπ)/8) ))) ....be continued...

$$\mathrm{let}\:\mathrm{try}\:\mathrm{another}\:\mathrm{way}\:\:\Phi=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{x}^{\mathrm{8}} \:+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{log}\left(\mathrm{x}^{\mathrm{8}} +\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{log}\left(\mathrm{x}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{1}\right)=\Phi \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{8a}^{\mathrm{7}} }{\left(\mathrm{x}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx}\:=\mathrm{8a}^{\mathrm{7}} \:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{x}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \:=\mathrm{0}\:\Rightarrow\left(\frac{\mathrm{x}}{\mathrm{a}}\right)^{\mathrm{8}} \:=−\mathrm{1}\:=\mathrm{e}^{\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}\pi} \:\Rightarrow\mathrm{x}^{\mathrm{8}} \:=\mathrm{a}^{\mathrm{8}} \:\mathrm{e}^{\left(\mathrm{2k}+\mathrm{1}\right)\mathrm{i}\pi} \:\Rightarrow \\ $$$$\mathrm{x}_{\mathrm{k}} =\mathrm{a}\:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\frac{\pi}{\mathrm{8}}} \:\Rightarrow\mathrm{x}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \:=\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \left(\mathrm{x}−\mathrm{a}\:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\frac{\pi}{\mathrm{8}}} \right) \\ $$$$\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \:\left(\mathrm{z}−\mathrm{ae}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\frac{\pi}{\mathrm{8}}} \right)} \\ $$$$\mathrm{z}_{\mathrm{k}} =\mathrm{ae}^{\frac{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{8}}} \:\Rightarrow\mathrm{z}_{\mathrm{0}} =\mathrm{a}\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{8}}} \:,\mathrm{z}_{\mathrm{1}} =\mathrm{ae}^{\mathrm{i}\frac{\mathrm{3}\pi}{\mathrm{8}}} \:,\mathrm{z}_{\mathrm{2}} =\mathrm{ae}^{\frac{\mathrm{i5}\pi}{\mathrm{8}}} \\ $$$$\mathrm{z}_{\mathrm{3}} =\mathrm{a}\:\mathrm{e}^{\frac{\mathrm{i7}\pi}{\mathrm{8}}} \:\:,\mathrm{z}_{\mathrm{4}} =\mathrm{ae}^{\frac{\mathrm{i9}\pi}{\mathrm{8}}} \:,\mathrm{z}_{\mathrm{5}} =\mathrm{ae}^{\frac{\mathrm{i11}\pi}{\mathrm{8}}} \:,\mathrm{z}_{\mathrm{6}} =\mathrm{ae}^{\frac{\mathrm{i13}\pi}{\mathrm{8}}} \:,\mathrm{z}_{\mathrm{7}} =\mathrm{ae}^{\frac{\mathrm{i15}\pi}{\mathrm{8}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\left\{\:\mathrm{Res}\left(\varphi,\mathrm{i}\right)+\mathrm{Res}\left(\varphi\:,\mathrm{ae}^{\frac{\mathrm{i}\pi}{\mathrm{8}}} \right)+\mathrm{Res}\left(\varphi,\mathrm{ae}^{\frac{\mathrm{i3}\pi}{\mathrm{8}}} \right)\right. \\ $$$$\left.+\mathrm{Res}\left(\varphi,\mathrm{a}\:\mathrm{e}^{\frac{\mathrm{i5}\pi}{\mathrm{8}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)=\frac{\mathrm{1}}{\mathrm{2i}\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \left(\mathrm{i}−\mathrm{ae}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\frac{\pi}{\mathrm{8}}} \right)} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{10}} \:+\mathrm{z}^{\mathrm{8}} \:+\mathrm{a}^{\mathrm{8}} \mathrm{z}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{8}} }=\frac{\mathrm{1}}{\mathrm{p}\left(\mathrm{z}\right)}\:\Rightarrow\mathrm{Res}\left(\varphi\:,\mathrm{z}_{\mathrm{i}} \right)\:=\frac{\mathrm{1}}{\mathrm{p}^{'} \left(\mathrm{z}_{\mathrm{i}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10z}_{\mathrm{i}} ^{\mathrm{9}} \:+\mathrm{8}\:\mathrm{z}_{\mathrm{i}} ^{\mathrm{7}} \:+\mathrm{2a}^{\mathrm{8}} \:\mathrm{z}_{\mathrm{i}} }\:\:\:\Rightarrow \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{ae}^{\frac{\mathrm{i}\pi}{\mathrm{8}}} \right)\:=\frac{\mathrm{1}}{\mathrm{10}\left(\mathrm{ae}^{\frac{\mathrm{i}\pi}{\mathrm{8}}} \right)^{\mathrm{9}} \:+\mathrm{8}\left(\mathrm{ae}^{\frac{\mathrm{i}\pi}{\mathrm{8}}} \right)^{\mathrm{7}} \:+\mathrm{2a}^{\mathrm{8}} \:\left(\mathrm{ae}^{\frac{\mathrm{i}\pi}{\mathrm{8}}} \right)} \\ $$$$....\mathrm{be}\:\mathrm{continued}... \\ $$

Answered by Dwaipayan Shikari last updated on 10/May/21

z=u^2 2∫_0 ^∞ ((log(1+u^8 ))/(1+u^2 )) =2∫_1 ^∞ ((log(1+u^8 ))/(1+u^2 ))du+2∫_0 ^1 ((log(1+u^8 ))/(1+u^2 ))du u=(1/j) =2∫_0 ^1 ((log(1+j^8 )−log(j^8 ))/(1+j^2 ))dj+2∫_0 ^1 ((log(1+u^8 ))/(1+u^2 ))du =4∫_0 ^1 ((log(1+j^8 ))/(1+j^2 ))−16∫_0 ^1 ((log(j))/(1+j^2 ))dj =4Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 j^(2n) log(1+j^8 )dj−∫_0 ^1 ((k^(−(3/4)) log(k))/(1−k))dk =4Σ_(n=0) ^∞ (−1)^n (((log(2))/(2n+1))−8∫_0 ^1 (j^(2n+8) /(1+j^8 ))dj)+ψ′((1/4)) =πlog(2)−32Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 ((j^(2n+8) −j^(2n+16) )/(1−j^(16) ))dj+ψ′((1/4)) =πlog(2)−2Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 ((k^((n/8)−(7/8)) −k^((n/8)+(1/8)) )/(1−k))dk+ψ′((1/4)) =πlog(2)−2Σ_(n=0) ^∞ (−1)^n (ψ((n/8)+(9/8))−ψ((n/8)+(1/8)))+ψ′((1/4)) =πlog(2)−2Σ_(n=0) ^∞ (−1)^n ((8/(n+1)))+ψ′((1/4)) =πlog(2)−16log(2)+ψ′((1/4))

$${z}={u}^{\mathrm{2}} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{log}\left(\mathrm{1}+{u}^{\mathrm{8}} \right)}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{1}} ^{\infty} \frac{{log}\left(\mathrm{1}+{u}^{\mathrm{8}} \right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{u}^{\mathrm{8}} \right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:\:\:{u}=\frac{\mathrm{1}}{{j}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{j}^{\mathrm{8}} \right)−{log}\left({j}^{\mathrm{8}} \right)}{\mathrm{1}+{j}^{\mathrm{2}} }{dj}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{u}^{\mathrm{8}} \right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}+{j}^{\mathrm{8}} \right)}{\mathrm{1}+{j}^{\mathrm{2}} }−\mathrm{16}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({j}\right)}{\mathrm{1}+{j}^{\mathrm{2}} }{dj} \\ $$$$=\mathrm{4}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {j}^{\mathrm{2}{n}} {log}\left(\mathrm{1}+{j}^{\mathrm{8}} \right){dj}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{k}^{−\frac{\mathrm{3}}{\mathrm{4}}} {log}\left({k}\right)}{\mathrm{1}−{k}}{dk} \\ $$$$=\mathrm{4}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left(\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}{n}+\mathrm{1}}−\mathrm{8}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{j}^{\mathrm{2}{n}+\mathrm{8}} }{\mathrm{1}+{j}^{\mathrm{8}} }{dj}\right)+\psi'\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\pi{log}\left(\mathrm{2}\right)−\mathrm{32}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{j}^{\mathrm{2}{n}+\mathrm{8}} −{j}^{\mathrm{2}{n}+\mathrm{16}} }{\mathrm{1}−{j}^{\mathrm{16}} }{dj}+\psi'\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\pi{log}\left(\mathrm{2}\right)−\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{k}^{\frac{{n}}{\mathrm{8}}−\frac{\mathrm{7}}{\mathrm{8}}} −{k}^{\frac{{n}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{8}}} }{\mathrm{1}−{k}}{dk}+\psi'\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\pi{log}\left(\mathrm{2}\right)−\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left(\psi\left(\frac{{n}}{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{8}}\right)−\psi\left(\frac{{n}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{8}}\right)\right)+\psi'\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\pi{log}\left(\mathrm{2}\right)−\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left(\frac{\mathrm{8}}{{n}+\mathrm{1}}\right)+\psi'\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\pi{log}\left(\mathrm{2}\right)−\mathrm{16}{log}\left(\mathrm{2}\right)+\psi'\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$

Commented by mathdanisur last updated on 11/May/21

Sir, answer 4πln((√2)+(√((2+(√2))))) simplify, psi(1/4) pliz

$$\left.{Sir},\:{answer}\:\mathrm{4}\pi{ln}\left(\sqrt{\mathrm{2}}+\sqrt{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right.}\right)\right) \\ $$$${simplify},\:{psi}\left(\mathrm{1}/\mathrm{4}\right)\:{pliz} \\ $$

Commented by mathdanisur last updated on 12/May/21

Sir, Dwaipayan Shikari pliz...

$${Sir},\:{Dwaipayan}\:{Shikari}\:{pliz}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com