Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 142310 by mathocean1 last updated on 29/May/21

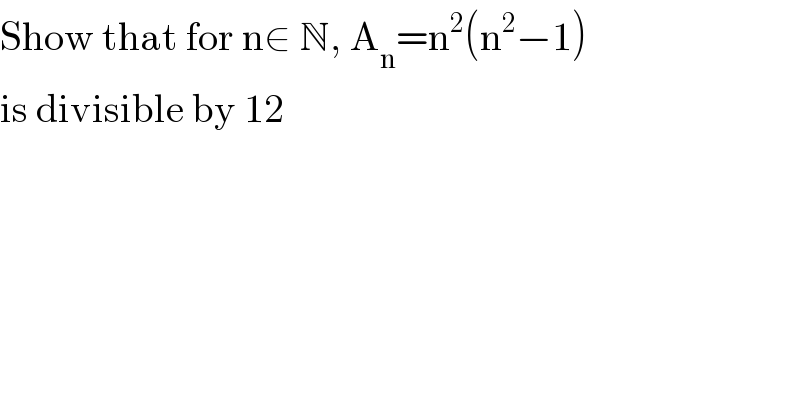
Show that for n∈ N, A_n =n^2 (n^2 −1) is divisible by 12

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{for}\:\mathrm{n}\in\:\mathbb{N},\:\mathrm{A}_{\mathrm{n}} =\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{12} \\ $$

Answered by MJS_new last updated on 29/May/21

A_(6k) =36k^2 (6k−1)(6k+1) A_(6k+1) =12k(3k+1)(6k+1)^2 A_(6k+2) =12(12k+1)(3k+1)^2 (6k+1) A_(6k+3) =36(2k+1)^2 (3k+1)(3k+2) A_(6k+4) =12(2k+1)(3k+2)^2 (6k+5) A_(6k+5) =12(k+1)(3k+2)(6k+5)^2

$${A}_{\mathrm{6}{k}} =\mathrm{36}{k}^{\mathrm{2}} \left(\mathrm{6}{k}−\mathrm{1}\right)\left(\mathrm{6}{k}+\mathrm{1}\right) \\ $$$${A}_{\mathrm{6}{k}+\mathrm{1}} =\mathrm{12}{k}\left(\mathrm{3}{k}+\mathrm{1}\right)\left(\mathrm{6}{k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${A}_{\mathrm{6}{k}+\mathrm{2}} =\mathrm{12}\left(\mathrm{12}{k}+\mathrm{1}\right)\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{6}{k}+\mathrm{1}\right) \\ $$$${A}_{\mathrm{6}{k}+\mathrm{3}} =\mathrm{36}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{3}{k}+\mathrm{1}\right)\left(\mathrm{3}{k}+\mathrm{2}\right) \\ $$$${A}_{\mathrm{6}{k}+\mathrm{4}} =\mathrm{12}\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{3}{k}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{6}{k}+\mathrm{5}\right) \\ $$$${A}_{\mathrm{6}{k}+\mathrm{5}} =\mathrm{12}\left({k}+\mathrm{1}\right)\left(\mathrm{3}{k}+\mathrm{2}\right)\left(\mathrm{6}{k}+\mathrm{5}\right)^{\mathrm{2}} \\ $$

Answered by JDamian last updated on 29/May/21

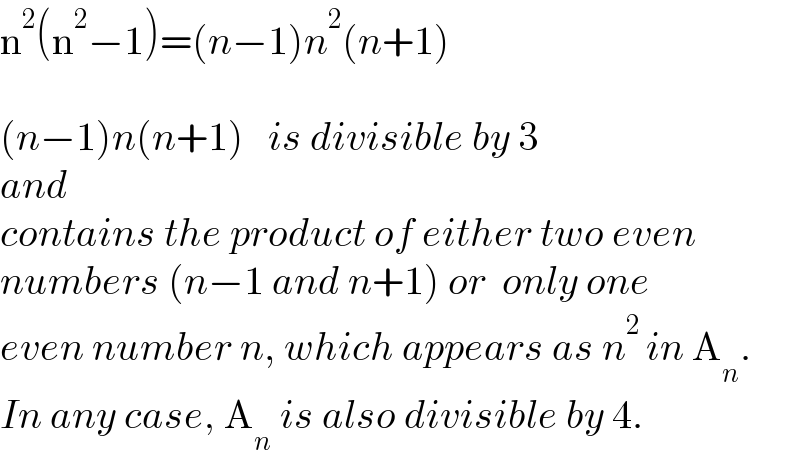
n^2 (n^2 −1)=(n−1)n^2 (n+1) (n−1)n(n+1) is divisible by 3 and contains the product of either two even numbers (n−1 and n+1) or only one even number n, which appears as n^2 in A_n . In any case, A_n is also divisible by 4.

$$\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right)=\left({n}−\mathrm{1}\right){n}^{\mathrm{2}} \left({n}+\mathrm{1}\right) \\ $$$$ \\ $$$$\left({n}−\mathrm{1}\right){n}\left({n}+\mathrm{1}\right)\:\:\:{is}\:{divisible}\:{by}\:\mathrm{3} \\ $$$${and} \\ $$$${contains}\:{the}\:{product}\:{of}\:{either}\:{two}\:{even} \\ $$$${numbers}\:\left({n}−\mathrm{1}\:{and}\:{n}+\mathrm{1}\right)\:{or}\:\:{only}\:{one} \\ $$$${even}\:{number}\:{n},\:{which}\:{appears}\:{as}\:{n}^{\mathrm{2}} \:{in}\:\mathrm{A}_{{n}} . \\ $$$${In}\:{any}\:{case},\:\mathrm{A}_{{n}} \:{is}\:{also}\:{divisible}\:{by}\:\mathrm{4}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com