Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 142545 by mnjuly1970 last updated on 02/Jun/21

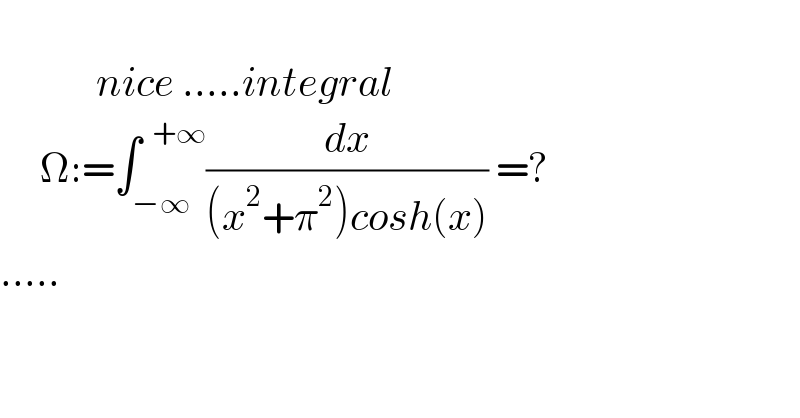
nice .....integral Ω:=∫_(−∞) ^( +∞) (dx/((x^2 +π^2 )cosh(x))) =? .....

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{nice}\:.....{integral} \\ $$$$\:\:\:\:\:\Omega:=\int_{−\infty} ^{\:\:+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\pi^{\mathrm{2}} \right){cosh}\left({x}\right)}\:=? \\ $$$$..... \\ $$

Answered by mindispower last updated on 02/Jun/21

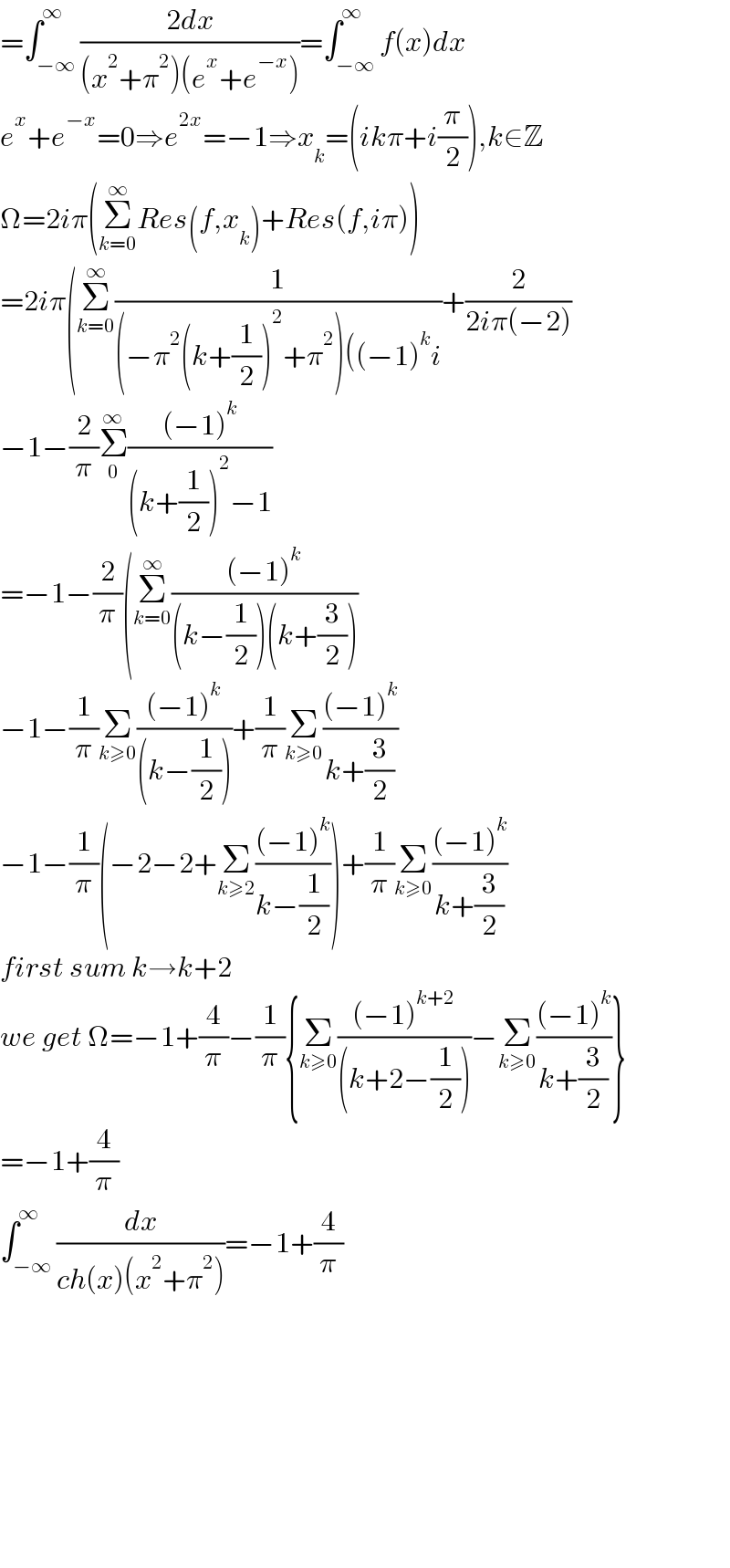
=∫_(−∞) ^∞ ((2dx)/((x^2 +π^2 )(e^x +e^(−x) )))=∫_(−∞) ^∞ f(x)dx e^x +e^(−x) =0⇒e^(2x) =−1⇒x_k =(ikπ+i(π/2)),k∈Z Ω=2iπ(Σ_(k=0) ^∞ Res(f,x_k )+Res(f,iπ)) =2iπ(Σ_(k=0) ^∞ (1/((−π^2 (k+(1/2))^2 +π^2 )((−1)^k i))+(2/(2iπ(−2))) −1−(2/π)Σ_0 ^∞ (((−1)^k )/((k+(1/2))^2 −1)) =−1−(2/π)(Σ_(k=0) ^∞ (((−1)^k )/((k−(1/2))(k+(3/2)))) −1−(1/π)Σ_(k≥0) (((−1)^k )/((k−(1/2))))+(1/π)Σ_(k≥0) (((−1)^k )/(k+(3/2))) −1−(1/π)(−2−2+Σ_(k≥2) (((−1)^k )/(k−(1/2))))+(1/π)Σ_(k≥0) (((−1)^k )/(k+(3/2))) first sum k→k+2 we get Ω=−1+(4/π)−(1/π){Σ_(k≥0) (((−1)^(k+2) )/((k+2−(1/2))))−Σ_(k≥0) (((−1)^k )/(k+(3/2)))} =−1+(4/π) ∫_(−∞) ^∞ (dx/(ch(x)(x^2 +π^2 )))=−1+(4/π)

$$=\int_{−\infty} ^{\infty} \frac{\mathrm{2}{dx}}{\left({x}^{\mathrm{2}} +\pi^{\mathrm{2}} \right)\left({e}^{{x}} +{e}^{−{x}} \right)}=\int_{−\infty} ^{\infty} {f}\left({x}\right){dx} \\ $$$${e}^{{x}} +{e}^{−{x}} =\mathrm{0}\Rightarrow{e}^{\mathrm{2}{x}} =−\mathrm{1}\Rightarrow{x}_{{k}} =\left({ik}\pi+{i}\frac{\pi}{\mathrm{2}}\right),{k}\in\mathbb{Z} \\ $$$$\Omega=\mathrm{2}{i}\pi\left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{Res}\left({f},{x}_{{k}} \right)+{Res}\left({f},{i}\pi\right)\right) \\ $$$$=\mathrm{2}{i}\pi\left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(−\pi^{\mathrm{2}} \left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\pi^{\mathrm{2}} \right)\left(\left(−\mathrm{1}\right)^{{k}} {i}\right.}+\frac{\mathrm{2}}{\mathrm{2}{i}\pi\left(−\mathrm{2}\right)}\right. \\ $$$$−\mathrm{1}−\frac{\mathrm{2}}{\pi}\underset{\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$=−\mathrm{1}−\frac{\mathrm{2}}{\pi}\left(\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({k}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\right. \\ $$$$−\mathrm{1}−\frac{\mathrm{1}}{\pi}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}−\frac{\mathrm{1}}{\mathrm{2}}\right)}+\frac{\mathrm{1}}{\pi}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$−\mathrm{1}−\frac{\mathrm{1}}{\pi}\left(−\mathrm{2}−\mathrm{2}+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}−\frac{\mathrm{1}}{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\pi}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$${first}\:{sum}\:{k}\rightarrow{k}+\mathrm{2} \\ $$$${we}\:{get}\:\Omega=−\mathrm{1}+\frac{\mathrm{4}}{\pi}−\frac{\mathrm{1}}{\pi}\left\{\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{2}} }{\left({k}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right)}−\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\frac{\mathrm{3}}{\mathrm{2}}}\right\} \\ $$$$=−\mathrm{1}+\frac{\mathrm{4}}{\pi} \\ $$$$\int_{−\infty} ^{\infty} \frac{{dx}}{{ch}\left({x}\right)\left({x}^{\mathrm{2}} +\pi^{\mathrm{2}} \right)}=−\mathrm{1}+\frac{\mathrm{4}}{\pi} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com