
Question Number 142880 by Dwaipayan Shikari last updated on 06/Jun/21
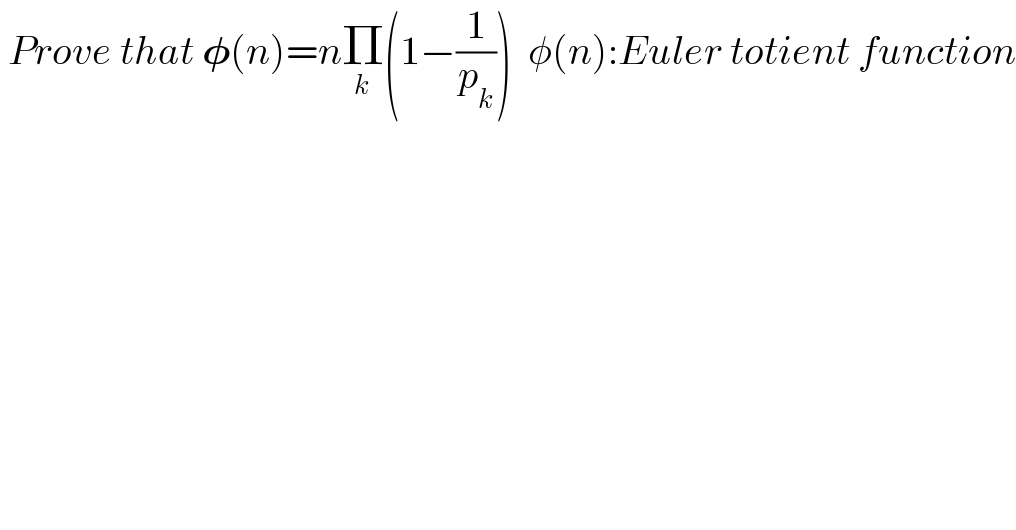
$$\:{Prove}\:{that}\:\boldsymbol{\phi}\left({n}\right)={n}\underset{{k}} {\prod}\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{{k}} }\right)\:\:\phi\left({n}\right):{Euler}\:{totient}\:{function} \\ $$
Answered by Snail last updated on 06/Jun/21
![I am considering that u know φ(n) is multiplicative function i.e φ(ab)=φ(a)φ(b)..where a and b are coprime Let p_1 .............p_k are distinct primd factors of n n=p_1 ^k_1 .........p_k ^k_r [here r=k as k=number of terms] φ(n)=φ(p_1 ^k_1 .....p_k ^k_r )=φ(p_1 ^k_1 )......φ(p_k ^k_r )....(1) Now the number of integers which are not coprime to p^(k ) ...(p.1),(p.2),(p.3),........(p.p^(k−1) ) φ(p^k )=numbdr of integers coprimd to p^k and<p^k = p^k −p^(k−1) =p^k (1−(1/p)) Now using this in( 1) =p_1 ^k_1 (1−(1/p_1 ))p_2 ^k_2 (1−(1/p_2 ))...p_k ^k_r (1−(1/p_r )) =p_1 ^k_1 p_2 ^k_2 .....p_r ^k_r (1−(1/p_1 )).....(1−(1/p_r )) =n(1−(1/p_1 ))(1−(1/p_2 ))....(1−(1/p_k )) Proved....](Q142892.png)
$${I}\:{am}\:{considering}\:{that}\:{u}\:{know}\:\phi\left({n}\right)\:{is}\:{multiplicative} \\ $$$${function}\:{i}.{e}\:\phi\left({ab}\right)=\phi\left({a}\right)\phi\left({b}\right)..{where}\:{a}\:{and}\:{b}\: \\ $$$${are}\:{coprime} \\ $$$${Let}\:{p}_{\mathrm{1}} .............{p}_{{k}} \:{are}\:{distinct}\:{primd}\:{factors}\:{of}\:\:{n} \\ $$$${n}={p}_{\mathrm{1}} ^{{k}_{\mathrm{1}} } .........{p}_{{k}} ^{{k}_{{r}} } \:\:\:\:\:\:\left[{here}\:{r}={k}\:{as}\:{k}={number}\:{of}\:{terms}\right] \\ $$$$\phi\left({n}\right)=\phi\left({p}_{\mathrm{1}} ^{{k}_{\mathrm{1}} } .....{p}_{{k}} ^{{k}_{{r}} } \right)=\phi\left({p}_{\mathrm{1}} ^{{k}_{\mathrm{1}} } \right)......\phi\left({p}_{{k}} ^{{k}_{{r}} } \right)....\left(\mathrm{1}\right) \\ $$$${Now}\:{the}\:{number}\:{of}\:{integers}\:{which}\:{are}\:{not} \\ $$$${coprime}\:{to}\:{p}^{{k}\:} ...\left({p}.\mathrm{1}\right),\left({p}.\mathrm{2}\right),\left({p}.\mathrm{3}\right),........\left({p}.{p}^{{k}−\mathrm{1}} \right) \\ $$$$\phi\left({p}^{{k}} \right)={numbdr}\:{of}\:{integers}\:{coprimd}\:{to}\:{p}^{{k}} {and}<{p}^{{k}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:{p}^{{k}} −{p}^{{k}−\mathrm{1}} ={p}^{{k}} \left(\mathrm{1}−\frac{\mathrm{1}}{{p}}\right) \\ $$$${Now}\:{using}\:{this}\:{in}\left(\:\mathrm{1}\right) \\ $$$$={p}_{\mathrm{1}} ^{{k}_{\mathrm{1}} } \left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{\mathrm{1}} }\right){p}_{\mathrm{2}} ^{{k}_{\mathrm{2}} } \left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{\mathrm{2}} }\right)...{p}_{{k}} ^{{k}_{{r}} } \left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{{r}} }\right) \\ $$$$ \\ $$$$={p}_{\mathrm{1}} ^{{k}_{\mathrm{1}} } {p}_{\mathrm{2}} ^{{k}_{\mathrm{2}} } .....{p}_{{r}} ^{{k}_{{r}} } \left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{\mathrm{1}} }\right).....\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{{r}} }\right) \\ $$$$={n}\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{\mathrm{1}} }\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{\mathrm{2}} }\right)....\left(\mathrm{1}−\frac{\mathrm{1}}{{p}_{{k}} }\right) \\ $$$${Proved}.... \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 07/Jun/21

$${Thanks} \\ $$
