Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 143098 by mnjuly1970 last updated on 10/Jun/21

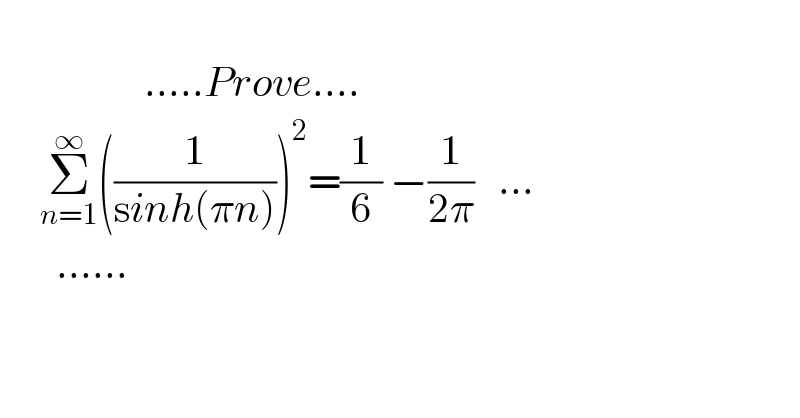
.....Prove.... Σ_(n=1) ^∞ ((1/(sinh(πn))))^2 =(1/6) −(1/(2π)) ... ......

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....{Prove}....\: \\ $$$$\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{s}{inh}\left(\pi{n}\right)}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{2}\pi}\:\:\:... \\ $$$$\:\:\:\:\:\:\:...... \\ $$

Answered by Dwaipayan Shikari last updated on 10/Jun/21

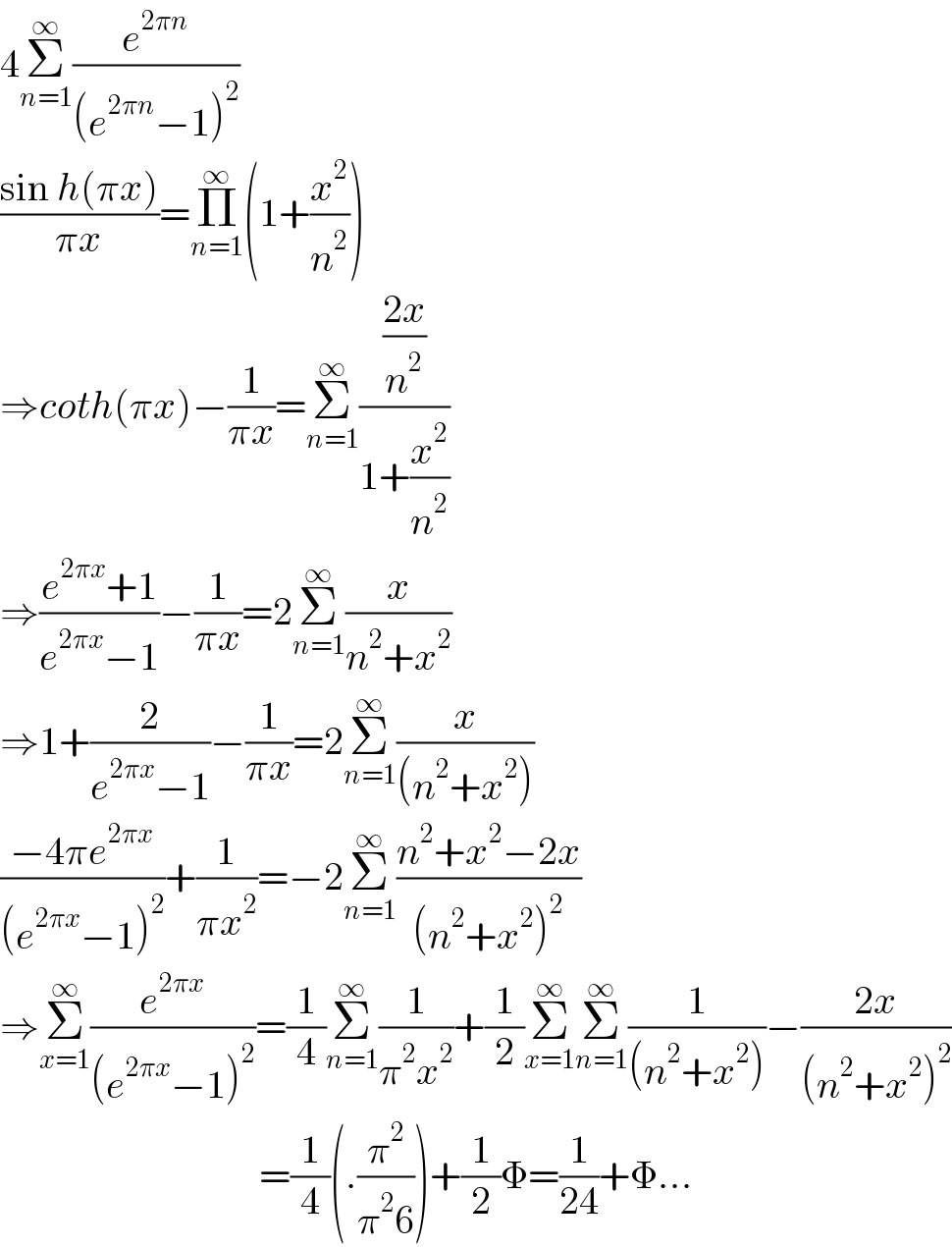
4Σ_(n=1) ^∞ (e^(2πn) /((e^(2πn) −1)^2 )) ((sin h(πx))/(πx))=Π_(n=1) ^∞ (1+(x^2 /n^2 )) ⇒coth(πx)−(1/(πx))=Σ_(n=1) ^∞ (((2x)/n^2 )/(1+(x^2 /n^2 ))) ⇒((e^(2πx) +1)/(e^(2πx) −1))−(1/(πx))=2Σ_(n=1) ^∞ (x/(n^2 +x^2 )) ⇒1+(2/(e^(2πx) −1))−(1/(πx))=2Σ_(n=1) ^∞ (x/((n^2 +x^2 ))) ((−4πe^(2πx) )/((e^(2πx) −1)^2 ))+(1/(πx^2 ))=−2Σ_(n=1) ^∞ ((n^2 +x^2 −2x)/((n^2 +x^2 )^2 )) ⇒Σ_(x=1) ^∞ (e^(2πx) /((e^(2πx) −1)^2 ))=(1/4)Σ_(n=1) ^∞ (1/(π^2 x^2 ))+(1/2)Σ_(x=1) ^∞ Σ_(n=1) ^∞ (1/((n^2 +x^2 )))−((2x)/((n^2 +x^2 )^2 )) =(1/4)(.(π^2 /(π^2 6)))+(1/2)Φ=(1/(24))+Φ...

$$\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{2}\pi{n}} }{\left({e}^{\mathrm{2}\pi{n}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{sin}\:{h}\left(\pi{x}\right)}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{coth}\left(\pi{x}\right)−\frac{\mathrm{1}}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\frac{\mathrm{2}{x}}{{n}^{\mathrm{2}} }}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{e}^{\mathrm{2}\pi{x}} +\mathrm{1}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\pi{x}}=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}}{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{1}+\frac{\mathrm{2}}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}−\frac{\mathrm{1}}{\pi{x}}=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)} \\ $$$$\frac{−\mathrm{4}\pi{e}^{\mathrm{2}\pi{x}} }{\left({e}^{\mathrm{2}\pi{x}} −\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\pi{x}^{\mathrm{2}} }=−\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{x}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{\mathrm{2}\pi{x}} }{\left({e}^{\mathrm{2}\pi{x}} −\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\pi^{\mathrm{2}} {x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\underset{{x}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)}−\frac{\mathrm{2}{x}}{\left({n}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(.\frac{\pi^{\mathrm{2}} }{\pi^{\mathrm{2}} \mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\Phi=\frac{\mathrm{1}}{\mathrm{24}}+\Phi... \\ $$

Commented by Dwaipayan Shikari last updated on 10/Jun/21

Sorry sir . I have tried

$${Sorry}\:{sir}\:.\:{I}\:\:{have}\:{tried}\: \\ $$

Commented by mnjuly1970 last updated on 10/Jun/21

grateful for your effort mr payan..

$$\:\:{grateful}\:{for}\:{your}\:{effort}\:{mr}\:{payan}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com