
Question Number 143995 by liberty last updated on 20/Jun/21
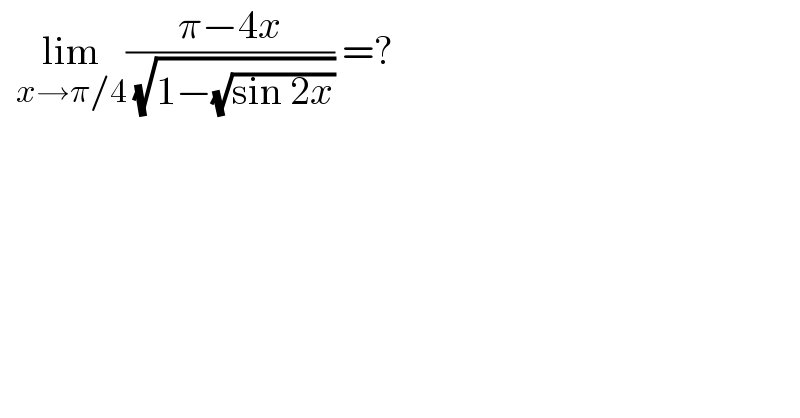
$$\:\:\underset{{x}\rightarrow\pi/\mathrm{4}} {\mathrm{lim}}\frac{\pi−\mathrm{4}{x}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{sin}\:\mathrm{2}{x}}}}\:=? \\ $$
Answered by mathmax by abdo last updated on 20/Jun/21
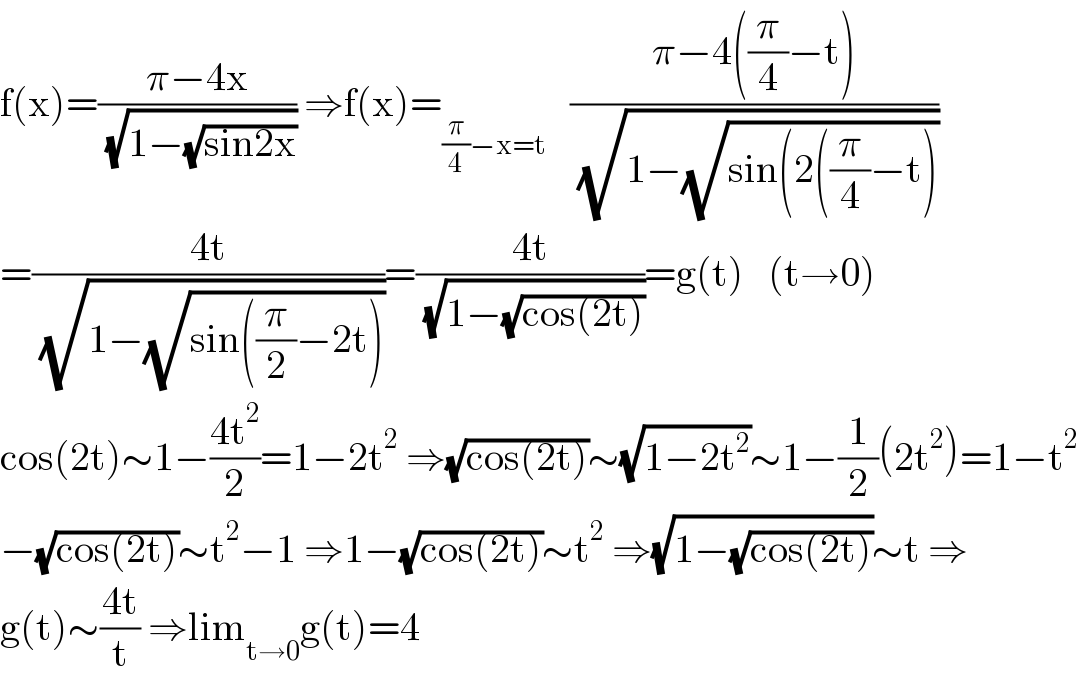
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\pi−\mathrm{4x}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{sin2x}}}}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=_{\frac{\pi}{\mathrm{4}}−\mathrm{x}=\mathrm{t}} \:\:\:\frac{\pi−\mathrm{4}\left(\frac{\pi}{\mathrm{4}}−\mathrm{t}\right)}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{sin}\left(\mathrm{2}\left(\frac{\pi}{\mathrm{4}}−\mathrm{t}\right)\right.}}} \\ $$$$=\frac{\mathrm{4t}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2t}\right)}}}=\frac{\mathrm{4t}}{\:\sqrt{\mathrm{1}−\sqrt{\mathrm{cos}\left(\mathrm{2t}\right)}}}=\mathrm{g}\left(\mathrm{t}\right)\:\:\:\left(\mathrm{t}\rightarrow\mathrm{0}\right) \\ $$$$\mathrm{cos}\left(\mathrm{2t}\right)\sim\mathrm{1}−\frac{\mathrm{4t}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{1}−\mathrm{2t}^{\mathrm{2}} \:\Rightarrow\sqrt{\mathrm{cos}\left(\mathrm{2t}\right)}\sim\sqrt{\mathrm{1}−\mathrm{2t}^{\mathrm{2}} }\sim\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2t}^{\mathrm{2}} \right)=\mathrm{1}−\mathrm{t}^{\mathrm{2}} \\ $$$$−\sqrt{\mathrm{cos}\left(\mathrm{2t}\right)}\sim\mathrm{t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\mathrm{1}−\sqrt{\mathrm{cos}\left(\mathrm{2t}\right)}\sim\mathrm{t}^{\mathrm{2}} \:\Rightarrow\sqrt{\mathrm{1}−\sqrt{\mathrm{cos}\left(\mathrm{2t}\right)}}\sim\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{t}\right)\sim\frac{\mathrm{4t}}{\mathrm{t}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)=\mathrm{4} \\ $$
Commented by liberty last updated on 21/Jun/21
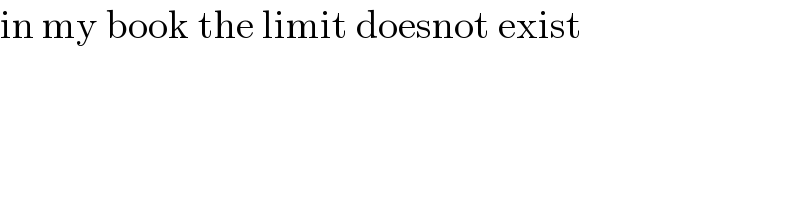
$$\mathrm{in}\:\mathrm{my}\:\mathrm{book}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{doesnot}\:\mathrm{exist} \\ $$
