
Question Number 144231 by mnjuly1970 last updated on 23/Jun/21
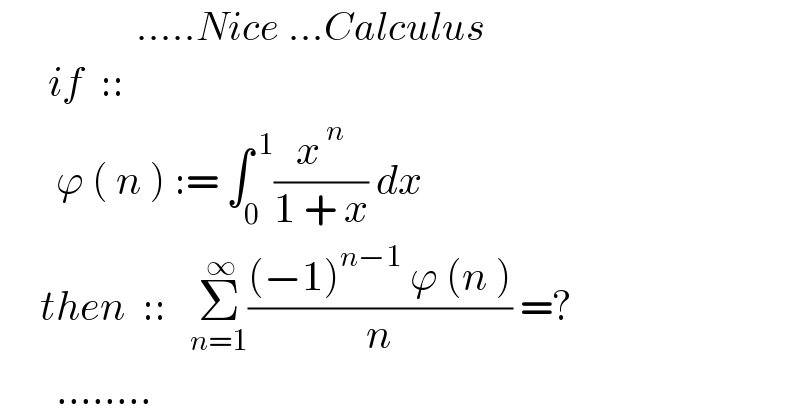
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....{Nice}\:...{Calculus} \\ $$$$\:\:\:\:\:\:{if}\:\:::\:\: \\ $$$$\:\:\:\:\:\:\:\varphi\:\left(\:{n}\:\right)\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\:{n}} }{\mathrm{1}\:+\:{x}}\:{dx} \\ $$$$\:\:\:\:\:{then}\:\:::\:\:\:\underset{{n}=\mathrm{1}} {\overset{\:\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\varphi\:\left({n}\:\right)}{{n}}\:=? \\ $$$$\:\:\:\:\:\:\:........ \\ $$
Answered by mathmax by abdo last updated on 23/Jun/21
![ϕ(n)=∫_0 ^1 (x^n /(1+x))dx ⇒let S=Σ_(n=1) ^∞ (((−1)^(n−1) )/n)ϕ(n) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^1 (x^n /(1+x))dx =∫_0 ^1 (Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(x^n /(1+x)))dx =∫_0 ^1 ((w(x))/(1+x))dx with w(x)=Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n ⇒ w^′ (x)=Σ_(n=1) ^∞ (−1)^(n−1) x^(n−1) =Σ_(n=1) ^∞ (−x)^(n−1) =Σ_(n=0) ^∞ (−x)^n =(1/(1+x)) ⇒w(x)=log(1+x)+c w(0)=0=c ⇒w(x)=log(1+x) ⇒ S=∫_0 ^1 ((log(1+x))/(1+x))dx =[log^2 (1+x)]_0 ^1 −∫_0 ^1 ((log(1+x))/(1+x))dx ⇒ 2∫_0 ^1 ((log(1+x))/(1+x))dx=log^2 (2) ⇒S=((log^2 (2))/2)](Q144240.png)
$$\varphi\left(\mathrm{n}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{let}\:\mathrm{S}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\varphi\left(\mathrm{n}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{w}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\mathrm{with}\:\:\mathrm{w}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\mathrm{x}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{w}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{x}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:\Rightarrow\mathrm{w}\left(\mathrm{x}\right)=\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)+\mathrm{c} \\ $$$$\mathrm{w}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{c}\:\Rightarrow\mathrm{w}\left(\mathrm{x}\right)=\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{S}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=\left[\mathrm{log}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}=\mathrm{log}^{\mathrm{2}} \left(\mathrm{2}\right)\:\Rightarrow\mathrm{S}=\frac{\mathrm{log}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 23/Jun/21
$$\:\:\:{thanks}\:{alot}\:{mr}\:{max}... \\ $$
Commented by mathmax by abdo last updated on 24/Jun/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
