Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 147035 by rs4089 last updated on 17/Jul/21

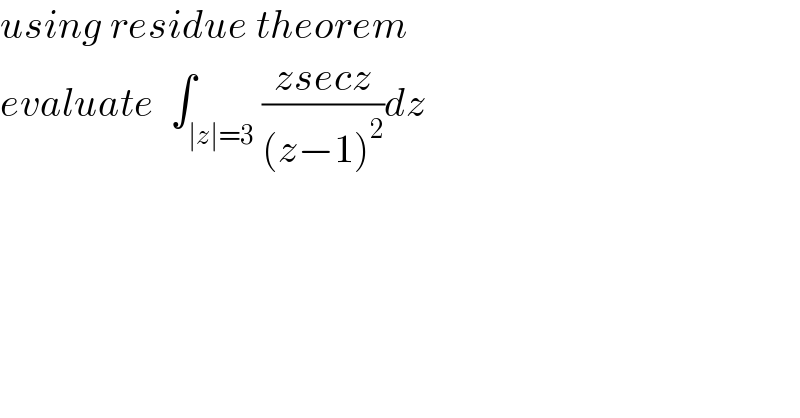
using residue theorem evaluate ∫_(∣z∣=3) ((zsecz)/((z−1)^2 ))dz

$${using}\:{residue}\:{theorem} \\ $$$${evaluate}\:\:\int_{\mid{z}\mid=\mathrm{3}} \frac{{zsecz}}{\left({z}−\mathrm{1}\right)^{\mathrm{2}} }{dz} \\ $$

Answered by mathmax by abdo last updated on 17/Jul/21

Ψ=∫_(∣z∣=3) (z/(cosz(z−1)^2 ))dz ⇒Ψ=2iπ Res(f,1) Res(f,1) =lim_(z→1) (1/((2−1)!)){(z−1)^2 f(z)}^((1)) =lim_(z→1) {(z/(cosz))}^((1)) =lim_(z→1) ((cosz+zsinz)/(cos^2 z))=((cos(1)+sin(1))/(cos^2 (1))) ⇒Ψ=2iπ×((cos(1)+sin(1))/(cos^2 (1)))

$$\Psi=\int_{\mid\mathrm{z}\mid=\mathrm{3}} \:\:\:\:\frac{\mathrm{z}}{\mathrm{cosz}\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dz}\:\Rightarrow\Psi=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{1}\right) \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{1}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{f}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \left\{\frac{\mathrm{z}}{\mathrm{cosz}}\right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{1}} \:\:\:\frac{\mathrm{cosz}+\mathrm{zsinz}}{\mathrm{cos}^{\mathrm{2}} \mathrm{z}}=\frac{\mathrm{cos}\left(\mathrm{1}\right)+\mathrm{sin}\left(\mathrm{1}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{1}\right)} \\ $$$$\Rightarrow\Psi=\mathrm{2i}\pi×\frac{\mathrm{cos}\left(\mathrm{1}\right)+\mathrm{sin}\left(\mathrm{1}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{1}\right)} \\ $$

Answered by Olaf_Thorendsen last updated on 17/Jul/21

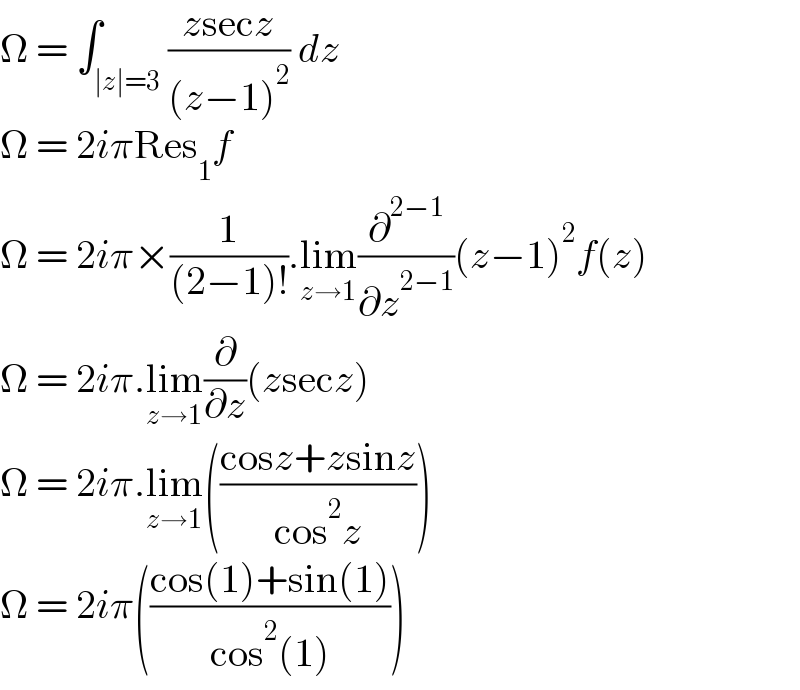
Ω = ∫_(∣z∣=3) ((zsecz)/((z−1)^2 )) dz Ω = 2iπRes_1 f Ω = 2iπ×(1/((2−1)!)).lim_(z→1) (∂^(2−1) /∂z^(2−1) )(z−1)^2 f(z) Ω = 2iπ.lim_(z→1) (∂/∂z)(zsecz) Ω = 2iπ.lim_(z→1) (((cosz+zsinz)/(cos^2 z))) Ω = 2iπ(((cos(1)+sin(1))/(cos^2 (1))))

$$\Omega\:=\:\int_{\mid{z}\mid=\mathrm{3}} \frac{{z}\mathrm{sec}{z}}{\left({z}−\mathrm{1}\right)^{\mathrm{2}} }\:{dz} \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi\mathrm{Res}_{\mathrm{1}} {f} \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi×\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}.\underset{{z}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\partial^{\mathrm{2}−\mathrm{1}} }{\partial{z}^{\mathrm{2}−\mathrm{1}} }\left({z}−\mathrm{1}\right)^{\mathrm{2}} {f}\left({z}\right) \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi.\underset{{z}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\partial}{\partial{z}}\left({z}\mathrm{sec}{z}\right) \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi.\underset{{z}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{cos}{z}+{z}\mathrm{sin}{z}}{\mathrm{cos}^{\mathrm{2}} {z}}\right) \\ $$$$\Omega\:=\:\mathrm{2}{i}\pi\left(\frac{\mathrm{cos}\left(\mathrm{1}\right)+\mathrm{sin}\left(\mathrm{1}\right)}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{1}\right)}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com