Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 147941 by mathdanisur last updated on 24/Jul/21

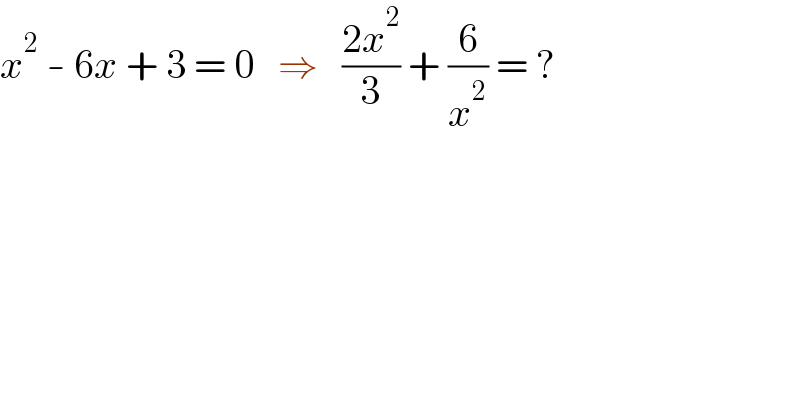
x^2 - 6x + 3 = 0 ⇒ ((2x^2 )/3) + (6/x^2 ) = ?

$${x}^{\mathrm{2}} \:-\:\mathrm{6}{x}\:+\:\mathrm{3}\:=\:\mathrm{0}\:\:\:\Rightarrow\:\:\:\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}}\:+\:\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\:=\:? \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jul/21

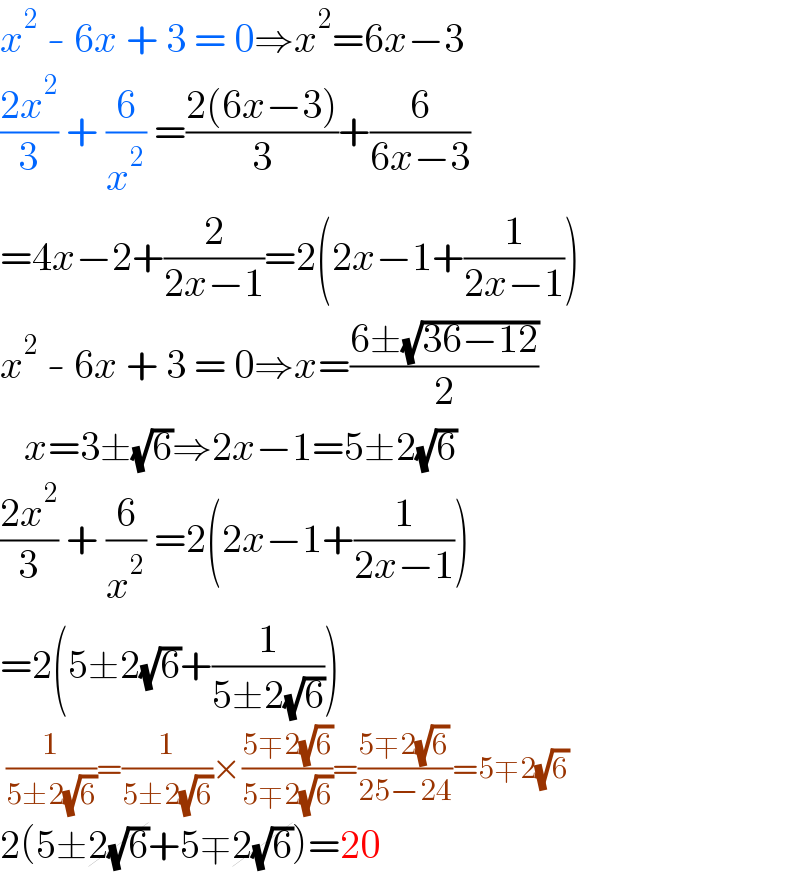
x^2 - 6x + 3 = 0⇒x^2 =6x−3 ((2x^2 )/3) + (6/x^2 ) =((2(6x−3))/3)+(6/(6x−3)) =4x−2+(2/(2x−1))=2(2x−1+(1/(2x−1))) x^2 - 6x + 3 = 0⇒x=((6±(√(36−12)))/2) x=3±(√6)⇒2x−1=5±2(√6) ((2x^2 )/3) + (6/x^2 ) =2(2x−1+(1/(2x−1))) =2(5±2(√6)+(1/(5±2(√6)))) (1/(5±2(√6)))=(1/(5±2(√6)))×((5∓2(√6))/(5∓2(√6)))=((5∓2(√6))/(25−24))=5∓2(√6) 2(5±2(√6)+5∓2(√6))=20

$${x}^{\mathrm{2}} \:-\:\mathrm{6}{x}\:+\:\mathrm{3}\:=\:\mathrm{0}\Rightarrow{x}^{\mathrm{2}} =\mathrm{6}{x}−\mathrm{3} \\ $$ $$\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}}\:+\:\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{2}\left(\mathrm{6}{x}−\mathrm{3}\right)}{\mathrm{3}}+\frac{\mathrm{6}}{\mathrm{6}{x}−\mathrm{3}} \\ $$ $$=\mathrm{4}{x}−\mathrm{2}+\frac{\mathrm{2}}{\mathrm{2}{x}−\mathrm{1}}=\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}\right) \\ $$ $${x}^{\mathrm{2}} \:-\:\mathrm{6}{x}\:+\:\mathrm{3}\:=\:\mathrm{0}\Rightarrow{x}=\frac{\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{12}}}{\mathrm{2}} \\ $$ $$\:\:\:{x}=\mathrm{3}\pm\sqrt{\mathrm{6}}\Rightarrow\mathrm{2}{x}−\mathrm{1}=\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$ $$\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}}\:+\:\frac{\mathrm{6}}{{x}^{\mathrm{2}} }\:=\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}\right) \\ $$ $$=\mathrm{2}\left(\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}}}\right) \\ $$ $$\:\frac{\mathrm{1}}{\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}}}=\frac{\mathrm{1}}{\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}}}×\frac{\mathrm{5}\mp\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}\mp\mathrm{2}\sqrt{\mathrm{6}}}=\frac{\mathrm{5}\mp\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{25}−\mathrm{24}}=\mathrm{5}\mp\mathrm{2}\sqrt{\mathrm{6}} \\ $$ $$\mathrm{2}\left(\mathrm{5}\pm\cancel{\mathrm{2}\sqrt{\mathrm{6}}}+\mathrm{5}\mp\cancel{\mathrm{2}\sqrt{\mathrm{6}}}\right)=\mathrm{20} \\ $$

Commented bymathdanisur last updated on 24/Jul/21

Thank you Ser

$${Thank}\:{you}\:{Ser} \\ $$

Answered by lyubita last updated on 25/Jul/21

x^2 + 3 = 6x x + (3/x) = 6 x^2 + (9/x^2 ) = 30 ((2x^2 )/3) + (6/x^(2 ) ) = 20

$${x}^{\mathrm{2}} \:+\:\mathrm{3}\:=\:\mathrm{6}{x} \\ $$ $${x}\:+\:\frac{\mathrm{3}}{{x}}\:=\:\mathrm{6} \\ $$ $${x}^{\mathrm{2}} \:+\:\frac{\mathrm{9}}{{x}^{\mathrm{2}} }\:=\:\mathrm{30} \\ $$ $$\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{3}}\:+\:\frac{\mathrm{6}}{{x}^{\mathrm{2}\:} }\:=\:\mathrm{20} \\ $$

Commented byRasheed.Sindhi last updated on 25/Jul/21

Nice!

$$\mathcal{N}{ice}! \\ $$

Commented bylyubita last updated on 25/Jul/21

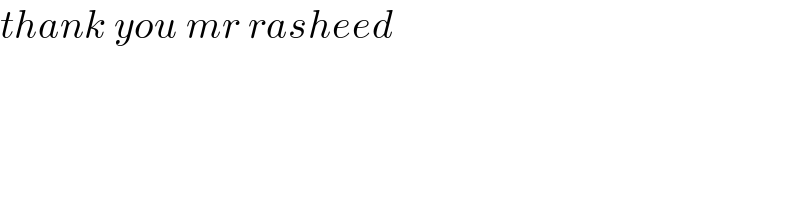
thank you mr rasheed

$${thank}\:{you}\:{mr}\:{rasheed} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com