
Question Number 147979 by mathdanisur last updated on 24/Jul/21
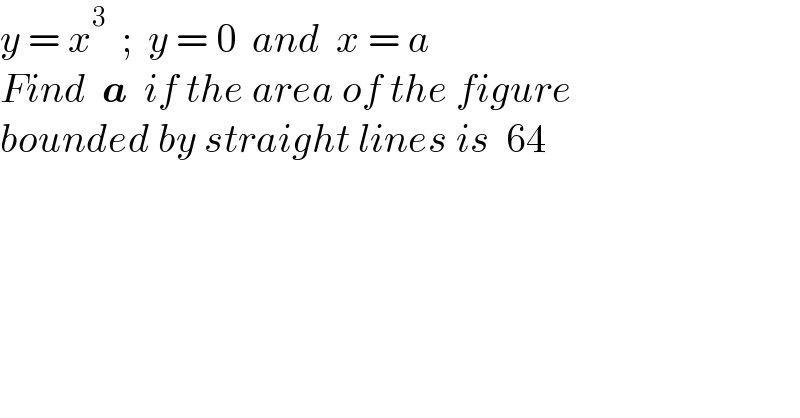
$${y}\:=\:{x}^{\mathrm{3}} \:\:;\:\:{y}\:=\:\mathrm{0}\:\:{and}\:\:{x}\:=\:{a} \\ $$$${Find}\:\:\boldsymbol{{a}}\:\:{if}\:{the}\:{area}\:{of}\:{the}\:{figure} \\ $$$${bounded}\:{by}\:{straight}\:{lines}\:{is}\:\:\mathrm{64} \\ $$
Answered by iloveisrael last updated on 25/Jul/21
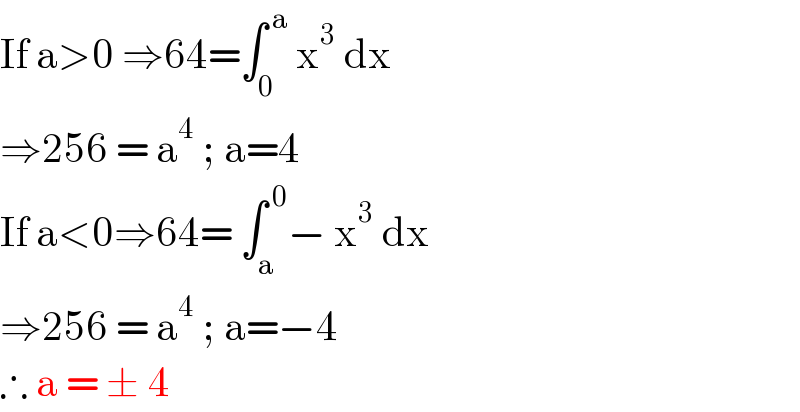
$$\mathrm{If}\:\mathrm{a}>\mathrm{0}\:\Rightarrow\mathrm{64}=\int_{\mathrm{0}} ^{\:\mathrm{a}} \:\mathrm{x}^{\mathrm{3}} \:\mathrm{dx}\: \\ $$$$\Rightarrow\mathrm{256}\:=\:\mathrm{a}^{\mathrm{4}} \:;\:\mathrm{a}=\mathrm{4} \\ $$$$\mathrm{If}\:\mathrm{a}<\mathrm{0}\Rightarrow\mathrm{64}=\:\int_{\mathrm{a}} ^{\:\mathrm{0}} −\:\mathrm{x}^{\mathrm{3}} \:\mathrm{dx}\: \\ $$$$\Rightarrow\mathrm{256}\:=\:\mathrm{a}^{\mathrm{4}} \:;\:\mathrm{a}=−\mathrm{4} \\ $$$$\therefore\:\mathrm{a}\:=\:\pm\:\mathrm{4}\: \\ $$
Commented by mathdanisur last updated on 25/Jul/21

$${Thankyou}\:{Ser} \\ $$
