Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148221 by 0731619 last updated on 26/Jul/21

Answered by Olaf_Thorendsen last updated on 26/Jul/21

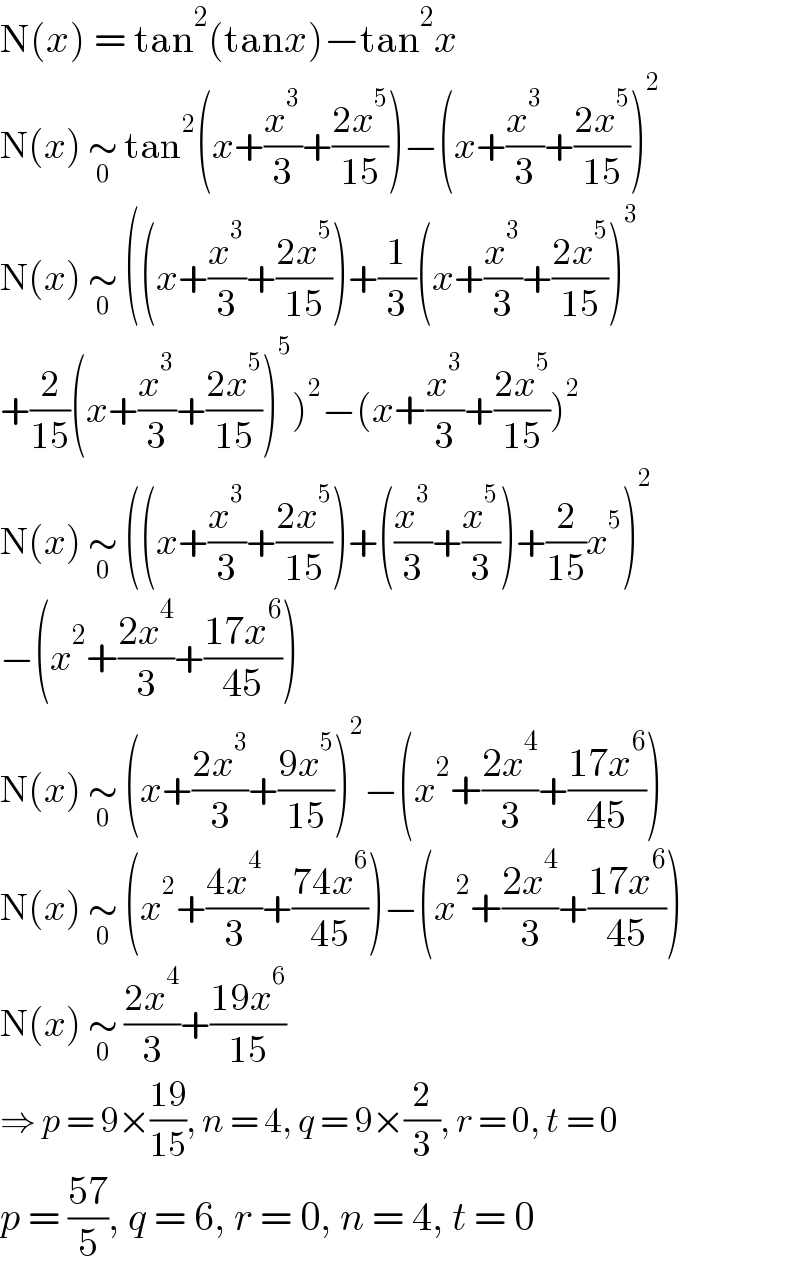
N(x) = tan^2 (tanx)−tan^2 x N(x) ∼_0 tan^2 (x+(x^3 /3)+((2x^5 )/(15)))−(x+(x^3 /3)+((2x^5 )/(15)))^2 N(x) ∼_0 ((x+(x^3 /3)+((2x^5 )/(15)))+(1/3)(x+(x^3 /3)+((2x^5 )/(15)))^3 +(2/(15))(x+(x^3 /3)+((2x^5 )/(15)))^5 )^2 −(x+(x^3 /3)+((2x^5 )/(15)))^2 N(x) ∼_0 ((x+(x^3 /3)+((2x^5 )/(15)))+((x^3 /3)+(x^5 /3))+(2/(15))x^5 )^2 −(x^2 +((2x^4 )/3)+((17x^6 )/(45))) N(x) ∼_0 (x+((2x^3 )/3)+((9x^5 )/(15)))^2 −(x^2 +((2x^4 )/3)+((17x^6 )/(45))) N(x) ∼_0 (x^2 +((4x^4 )/3)+((74x^6 )/(45)))−(x^2 +((2x^4 )/3)+((17x^6 )/(45))) N(x) ∼_0 ((2x^4 )/3)+((19x^6 )/(15)) ⇒ p = 9×((19)/(15)), n = 4, q = 9×(2/3), r = 0, t = 0 p = ((57)/5), q = 6, r = 0, n = 4, t = 0

$$\mathrm{N}\left({x}\right)\:=\:\mathrm{tan}^{\mathrm{2}} \left(\mathrm{tan}{x}\right)−\mathrm{tan}^{\mathrm{2}} {x} \\ $$$$\mathrm{N}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\mathrm{tan}^{\mathrm{2}} \left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)−\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)^{\mathrm{2}} \\ $$$$\mathrm{N}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\left(\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)^{\mathrm{3}} \right. \\ $$$$\left.+\frac{\mathrm{2}}{\mathrm{15}}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)^{\mathrm{5}} \right)^{\mathrm{2}} −\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)^{\mathrm{2}} \\ $$$$\mathrm{N}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\left(\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)+\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{5}} }{\mathrm{3}}\right)+\frac{\mathrm{2}}{\mathrm{15}}{x}^{\mathrm{5}} \right)^{\mathrm{2}} \\ $$$$−\left({x}^{\mathrm{2}} +\frac{\mathrm{2}{x}^{\mathrm{4}} }{\mathrm{3}}+\frac{\mathrm{17}{x}^{\mathrm{6}} }{\mathrm{45}}\right) \\ $$$$\mathrm{N}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\left({x}+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{9}{x}^{\mathrm{5}} }{\mathrm{15}}\right)^{\mathrm{2}} −\left({x}^{\mathrm{2}} +\frac{\mathrm{2}{x}^{\mathrm{4}} }{\mathrm{3}}+\frac{\mathrm{17}{x}^{\mathrm{6}} }{\mathrm{45}}\right) \\ $$$$\mathrm{N}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\left({x}^{\mathrm{2}} +\frac{\mathrm{4}{x}^{\mathrm{4}} }{\mathrm{3}}+\frac{\mathrm{74}{x}^{\mathrm{6}} }{\mathrm{45}}\right)−\left({x}^{\mathrm{2}} +\frac{\mathrm{2}{x}^{\mathrm{4}} }{\mathrm{3}}+\frac{\mathrm{17}{x}^{\mathrm{6}} }{\mathrm{45}}\right) \\ $$$$\mathrm{N}\left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{2}{x}^{\mathrm{4}} }{\mathrm{3}}+\frac{\mathrm{19}{x}^{\mathrm{6}} }{\mathrm{15}} \\ $$$$\Rightarrow\:{p}\:=\:\mathrm{9}×\frac{\mathrm{19}}{\mathrm{15}},\:{n}\:=\:\mathrm{4},\:{q}\:=\:\mathrm{9}×\frac{\mathrm{2}}{\mathrm{3}},\:{r}\:=\:\mathrm{0},\:{t}\:=\:\mathrm{0} \\ $$$${p}\:=\:\frac{\mathrm{57}}{\mathrm{5}},\:{q}\:=\:\mathrm{6},\:{r}\:=\:\mathrm{0},\:{n}\:=\:\mathrm{4},\:{t}\:=\:\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com