Math Question and Answers


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 148222 by BHOOPENDRA last updated on 26/Jul/21

	Answered by iloveisrael last updated on 26/Jul/21
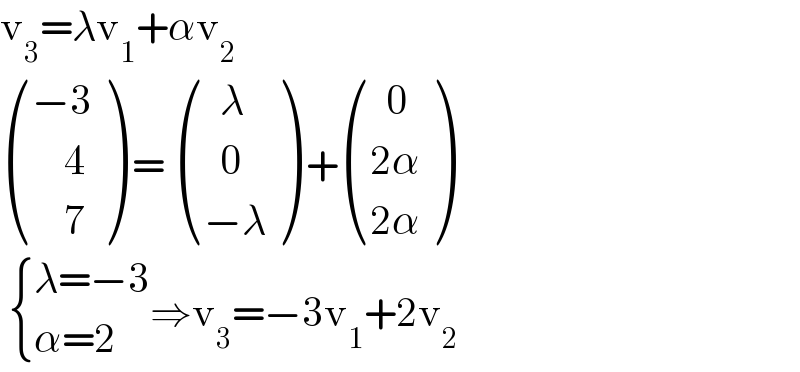
	$v_3 =λv_1 +αv_2 (((−3)),(( 4)),(( 7)) ) = ((( λ)),(( 0)),((−λ)) ) + ((( 0)),((2α)),((2α)) ) { ((λ=−3)),((α=2)) :}⇒v_3 =−3v_1 +2v_2$
	$v_{3} = λ v_{1} + α v_{2}$ $(\begin{matrix} - 3 \\ 4 \\ 7 \end{matrix}) = (\begin{matrix} λ \\ 0 \\ - λ \end{matrix}) + (\begin{matrix} 0 \\ 2 α \\ 2 α \end{matrix})$ ${\begin{cases} λ = - 3 \\ α = 2 \end{cases} \Rightarrow v_{3} = - {3 v}_{1} + {2 v}_{2}$
	Commented by BHOOPENDRA last updated on 26/Jul/21

	$w h a t a b o u t t h e o t h e r t w o s i r ?$
	Answered by Olaf_Thorendsen last updated on 26/Jul/21
	$(ii) Let v = ((x),(y),(z) ) ∈ W then ∃(α,β,γ)∈R^3 \ v = αv_1 +αv_2 +γv_3 v = αv_1 +βv_2 +γ(−3v_1 +2v_2 ) v = (α−3γ)v_1 +(β+2γ)v_2 Let a = α−3γ and b = β+2γ then ∃(a,b)∈R^2 \ v = av_1 +bv_2 That proves that (v_1 ,v_2 ) generates W. (iii) We solve the equation λv_1 +μv_2 = 0_W (1) ⇔ λ ((1),(0),((−1)) )+μ ((0),(2),(2) ) = ((0),(0),(0) ) ⇔ (λ,μ) = (0,0) We canno′t find (λ,μ)∈R^2 −{(0,0)} such that (1) is true. That proves that v_1 and v_2 are linearly independent.$
	$(ii)$ $Let v = (\begin{matrix} x \\ y \\ z \end{matrix}) \in W$ $then \exists (α, β, γ) \in R^{3} ∖ v = α v_{1} + α v_{2} + γ v_{3}$ $v = α v_{1} + β v_{2} + γ (- 3 v_{1} + 2 v_{2})$ $v = (α - 3 γ) v_{1} + (β + 2 γ) v_{2}$ $Let a = α - 3 γ and b = β + 2 γ$ $then \exists (a, b) \in R^{2} ∖ v = {a v}_{1} + {b v}_{2}$ $That proves that (v_{1}, v_{2}) generates W .$ $(iii)$ $We solve the equation$ $λ v_{1} + μ v_{2} = 0_{W} (1)$ $\Leftrightarrow λ (\begin{matrix} 1 \\ 0 \\ - 1 \end{matrix}) + μ (\begin{matrix} 0 \\ 2 \\ 2 \end{matrix}) = (\begin{matrix} 0 \\ 0 \\ 0 \end{matrix})$ $\Leftrightarrow (λ, μ) = (0, 0)$ $We {canno}^{'} t find (λ, μ) \in R^{2} - {(0, 0)}$ $such that (1) is true .$ $That proves that v_{1} and v_{2} are$ $linearly independent .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum