Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148241 by 7770 last updated on 26/Jul/21

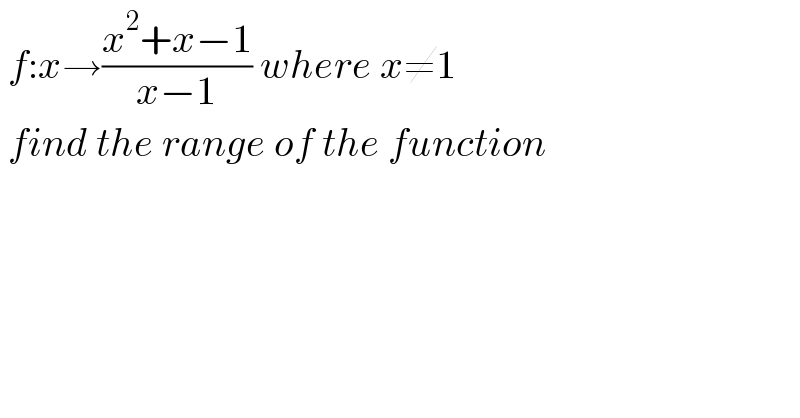
f:x→((x^2 +x−1)/(x−1)) where x≠1 find the range of the function

$$\:{f}:{x}\rightarrow\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}−\mathrm{1}}\:{where}\:{x}\neq\mathrm{1} \\ $$$$\:{find}\:{the}\:{range}\:{of}\:{the}\:{function} \\ $$

Answered by Olaf_Thorendsen last updated on 26/Jul/21

f(x) = ((x^2 +x−1)/(x−1)) = x+2+(1/(x−1)) lim_(x→±∞) f(x) = ±∞, limf(x) = ±∞_(x→1^± ) f′(x) = 1−(1/((x−1)^2 )) f′(x) = 0 ⇔ x = 2 f(0) = 1 and f(2) = 5 ∀x∈]0,1[∪]1,2[, f′(x) < 0 ∀x∈]−∞,0[∪]2,+∞[, f′(x) > 0 f(]−∞,0]) = ]−∞,1] f([0,1[) = [−∞,1] f(]1,2]) = [5,+∞] f([2,+∞[) = [5,+∞] • f(R\{1}) = R\]1,5[

$${f}\left({x}\right)\:=\:\frac{{x}^{\mathrm{2}} +{x}−\mathrm{1}}{{x}−\mathrm{1}}\:=\:{x}+\mathrm{2}+\frac{\mathrm{1}}{{x}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\pm\infty} {\mathrm{lim}}{f}\left({x}\right)\:=\:\pm\infty,\:\underset{{x}\rightarrow\mathrm{1}^{\pm} } {\mathrm{lim}{f}\left({x}\right)\:=\:\pm\infty} \\ $$$$ \\ $$$${f}'\left({x}\right)\:=\:\mathrm{1}−\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${f}'\left({x}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:{x}\:=\:\mathrm{2} \\ $$$${f}\left(\mathrm{0}\right)\:=\:\mathrm{1}\:\mathrm{and}\:{f}\left(\mathrm{2}\right)\:=\:\mathrm{5} \\ $$$$\left.\forall{x}\in\right]\mathrm{0},\mathrm{1}\left[\cup\right]\mathrm{1},\mathrm{2}\left[,\:{f}'\left({x}\right)\:<\:\mathrm{0}\:\right. \\ $$$$\left.\forall{x}\in\right]−\infty,\mathrm{0}\left[\cup\right]\mathrm{2},+\infty\left[,\:{f}'\left({x}\right)\:>\:\mathrm{0}\right. \\ $$$$ \\ $$$$\left.{f}\left.\left(\left.\right]\left.−\infty,\mathrm{0}\right]\right)\:=\:\right]−\infty,\mathrm{1}\right] \\ $$$${f}\left(\left[\mathrm{0},\mathrm{1}\left[\right)\:=\:\left[−\infty,\mathrm{1}\right]\right.\right. \\ $$$$\left.{f}\left.\left(\right]\mathrm{1},\mathrm{2}\right]\right)\:=\:\left[\mathrm{5},+\infty\right] \\ $$$${f}\left(\left[\mathrm{2},+\infty\left[\right)\:=\:\left[\mathrm{5},+\infty\right]\right.\right. \\ $$$$ \\ $$$$\left.\bullet\:{f}\left(\mathbb{R}\backslash\left\{\mathrm{1}\right\}\right)\:=\:\mathbb{R}\backslash\right]\mathrm{1},\mathrm{5}\left[\right. \\ $$$$ \\ $$

Answered by liberty last updated on 26/Jul/21

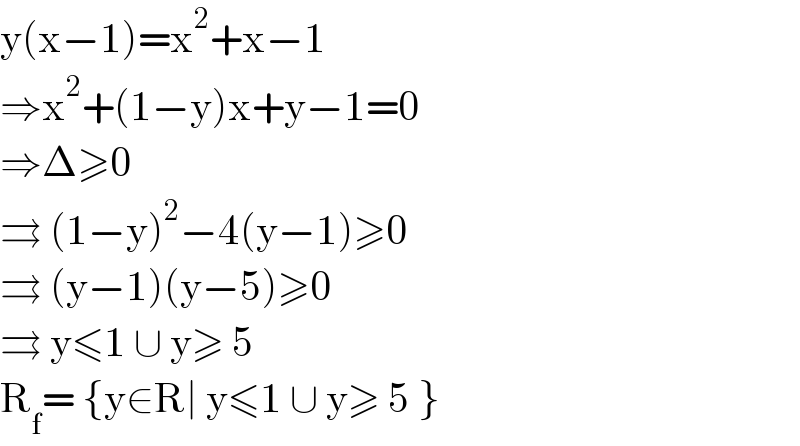
y(x−1)=x^2 +x−1 ⇒x^2 +(1−y)x+y−1=0 ⇒Δ≥0 ⇉ (1−y)^2 −4(y−1)≥0 ⇉ (y−1)(y−5)≥0 ⇉ y≤1 ∪ y≥ 5 R_f = {y∈R∣ y≤1 ∪ y≥ 5 }

$$\mathrm{y}\left(\mathrm{x}−\mathrm{1}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{y}\right)\mathrm{x}+\mathrm{y}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\Delta\geqslant\mathrm{0}\: \\ $$$$\rightrightarrows\:\left(\mathrm{1}−\mathrm{y}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{y}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\rightrightarrows\:\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}−\mathrm{5}\right)\geqslant\mathrm{0} \\ $$$$\rightrightarrows\:\mathrm{y}\leqslant\mathrm{1}\:\cup\:\mathrm{y}\geqslant\:\mathrm{5} \\ $$$$\mathrm{R}_{\mathrm{f}} =\:\left\{\mathrm{y}\in\mathrm{R}\mid\:\mathrm{y}\leqslant\mathrm{1}\:\cup\:\mathrm{y}\geqslant\:\mathrm{5}\:\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com