Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 148268 by mathdanisur last updated on 26/Jul/21

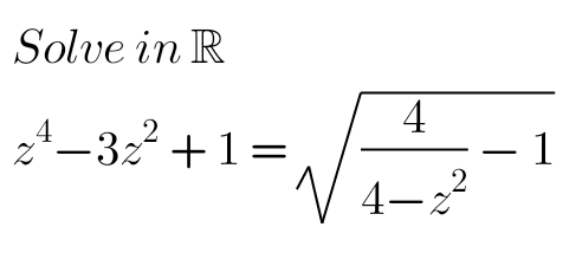
Answered by Olaf_Thorendsen last updated on 26/Jul/21

z^4 −3z^2 +1 = (√((4/(4−z^2 ))−1)) (1) Let w = z^2 (1) : w^2 −3w+1 = (√((4/(4−w))−1)) ⇒ (∗) w^4 −6w^3 +11w^2 −6w+1 = (w/(4−w)) w^5 −10w^4 +35w^3 −50w^2 +26w−4 = 0 (w^5 −2w^4 )−8(w^4 −2w^3 )+19(w^3 −2w^2 ) −12(w^2 −2w)+2(w−2) = 0 w^4 (w−2)−8w^3 (w−2)+19w^2 (w−2) −12w(w−2)+2(w−2) = 0 (w−2)(w^4 −8w^3 +19w^2 −12w+2) = 0 (w−2)(w^2 +pw+2)(w^2 +qw+1) = 0 By identification p = q = −4 (w−2)(w^2 −4w+2)(w^2 −4w+1) = 0 (w−2)(w−(2−(√2)))(w−(2+(√2))(w−(2−(√3)))(w−(2+(√3))) = 0 w = 2, w = 2±(√2), w = 2±(√3) ⇒z = ±(√2), z = ±(√(2±(√2))), z = ±(√(2±(√3))) (∗) Because of ⇒ we have to verify each solution. ±(√2) and ±(√(2−(√2))) are not good. S = {±(√(2+(√2))), ±(√(2±(√3)))}

$${z}^{\mathrm{4}} −\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}\:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{4}−{z}^{\mathrm{2}} }−\mathrm{1}}\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:{w}\:=\:{z}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\::\:{w}^{\mathrm{2}} −\mathrm{3}{w}+\mathrm{1}\:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{4}−{w}}−\mathrm{1}} \\ $$$$\Rightarrow\:\left(\ast\right)\:{w}^{\mathrm{4}} −\mathrm{6}{w}^{\mathrm{3}} +\mathrm{11}{w}^{\mathrm{2}} −\mathrm{6}{w}+\mathrm{1}\:=\:\frac{{w}}{\mathrm{4}−{w}} \\ $$$${w}^{\mathrm{5}} −\mathrm{10}{w}^{\mathrm{4}} +\mathrm{35}{w}^{\mathrm{3}} −\mathrm{50}{w}^{\mathrm{2}} +\mathrm{26}{w}−\mathrm{4}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\left({w}^{\mathrm{5}} −\mathrm{2}{w}^{\mathrm{4}} \right)−\mathrm{8}\left({w}^{\mathrm{4}} −\mathrm{2}{w}^{\mathrm{3}} \right)+\mathrm{19}\left({w}^{\mathrm{3}} −\mathrm{2}{w}^{\mathrm{2}} \right) \\ $$$$−\mathrm{12}\left({w}^{\mathrm{2}} −\mathrm{2}{w}\right)+\mathrm{2}\left({w}−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$${w}^{\mathrm{4}} \left({w}−\mathrm{2}\right)−\mathrm{8}{w}^{\mathrm{3}} \left({w}−\mathrm{2}\right)+\mathrm{19}{w}^{\mathrm{2}} \left({w}−\mathrm{2}\right) \\ $$$$−\mathrm{12}{w}\left({w}−\mathrm{2}\right)+\mathrm{2}\left({w}−\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$ \\ $$$$\left({w}−\mathrm{2}\right)\left({w}^{\mathrm{4}} −\mathrm{8}{w}^{\mathrm{3}} +\mathrm{19}{w}^{\mathrm{2}} −\mathrm{12}{w}+\mathrm{2}\right)\:=\:\mathrm{0} \\ $$$$\left({w}−\mathrm{2}\right)\left({w}^{\mathrm{2}} +{pw}+\mathrm{2}\right)\left({w}^{\mathrm{2}} +{qw}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{By}\:\mathrm{identification}\:{p}\:=\:{q}\:=\:−\mathrm{4} \\ $$$$\left({w}−\mathrm{2}\right)\left({w}^{\mathrm{2}} −\mathrm{4}{w}+\mathrm{2}\right)\left({w}^{\mathrm{2}} −\mathrm{4}{w}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\left({w}−\mathrm{2}\right)\left({w}−\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\right)\left({w}−\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\left({w}−\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\right)\left({w}−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\right)\:=\:\mathrm{0}\right. \\ $$$$ \\ $$$${w}\:=\:\mathrm{2},\:{w}\:=\:\mathrm{2}\pm\sqrt{\mathrm{2}},\:{w}\:=\:\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\Rightarrow{z}\:=\:\pm\sqrt{\mathrm{2}},\:{z}\:=\:\pm\sqrt{\mathrm{2}\pm\sqrt{\mathrm{2}}},\:{z}\:=\:\pm\sqrt{\mathrm{2}\pm\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$\left(\ast\right)\:\mathrm{Because}\:\mathrm{of}\:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{verify} \\ $$$$\mathrm{each}\:\mathrm{solution}.\:\pm\sqrt{\mathrm{2}}\:\mathrm{and}\:\pm\sqrt{\mathrm{2}−\sqrt{\mathrm{2}}}\: \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{good}. \\ $$$$ \\ $$$$\mathcal{S}\:=\:\left\{\pm\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}},\:\pm\sqrt{\mathrm{2}\pm\sqrt{\mathrm{3}}}\right\} \\ $$$$ \\ $$

Commented by mathdanisur last updated on 26/Jul/21

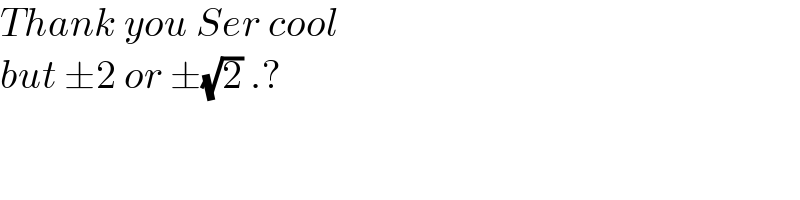
Thank you Ser cool but ±2 or ±(√2) .?

$${Thank}\:{you}\:{Ser}\:{cool} \\ $$$${but}\:\pm\mathrm{2}\:{or}\:\pm\sqrt{\mathrm{2}}\:.? \\ $$

Commented by Olaf_Thorendsen last updated on 26/Jul/21

I corrected sir.

$$\mathrm{I}\:\mathrm{corrected}\:\mathrm{sir}. \\ $$

Commented by mathdanisur last updated on 26/Jul/21

Thanks Ser

$${Thanks}\:{Ser} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com