Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 148303 by mathmax by abdo last updated on 26/Jul/21

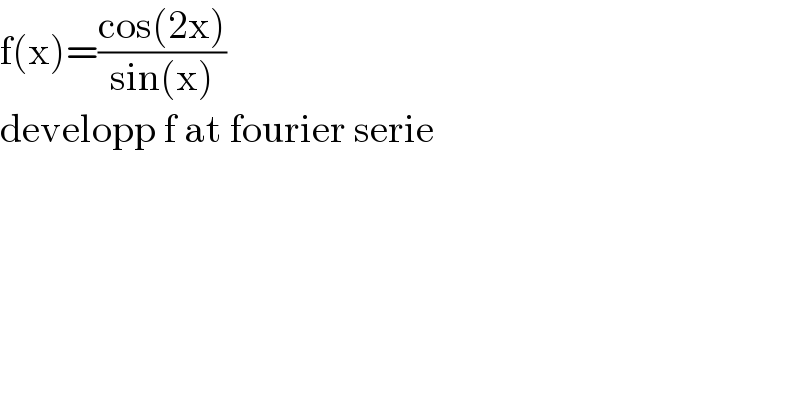
f(x)=((cos(2x))/(sin(x))) developp f at fourier serie

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{sin}\left(\mathrm{x}\right)} \\ $$$$\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Answered by Olaf_Thorendsen last updated on 27/Jul/21

f(x) = ((cos(2x))/(sinx)) cos(2x) = Σ_(n=1) ^∞ (cos((2nx)−cos(2(n+1)x) (telescopic sum) cos(2x) = Σ_(n=1) ^∞ (cos((2n+1)x−x)−cos((2n+1)x+x) cos(2x) = 2Σ_(n=1) ^∞ (1/2)(cos((2n+1)x−x)−cos((2n+1)x+x) cos(2x) = 2Σ_(n=1) ^∞ sin((2n+1)x).sinx ((cos(2x))/(sinx)) = 2Σ_(n=1) ^∞ sin((2n+1)x) a_0 = 0 and ∀n≥1, a_n = 0 (because f is odd) ∀n∈N^∗ , b_(2n) = 0 and ∀n∈N, b_(2n+1) = 2

$${f}\left({x}\right)\:=\:\frac{\mathrm{cos}\left(\mathrm{2}{x}\right)}{\mathrm{sin}{x}} \\ $$$$\mathrm{cos}\left(\mathrm{2}{x}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\mathrm{cos}\left(\left(\mathrm{2}{nx}\right)−\mathrm{cos}\left(\mathrm{2}\left({n}+\mathrm{1}\right){x}\right)\right.\right. \\ $$$$\left(\mathrm{telescopic}\:\mathrm{sum}\right) \\ $$$$\mathrm{cos}\left(\mathrm{2}{x}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\mathrm{cos}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}−{x}\right)−\mathrm{cos}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}+{x}\right)\right. \\ $$$$\mathrm{cos}\left(\mathrm{2}{x}\right)\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}−{x}\right)−\mathrm{cos}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}+{x}\right)\right. \\ $$$$\mathrm{cos}\left(\mathrm{2}{x}\right)\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{sin}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}\right).\mathrm{sin}{x} \\ $$$$ \\ $$$$\frac{\mathrm{cos}\left(\mathrm{2}{x}\right)}{\mathrm{sin}{x}}\:=\:\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{sin}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}\right) \\ $$$$ \\ $$$${a}_{\mathrm{0}} \:=\:\mathrm{0}\:{and}\:\forall{n}\geqslant\mathrm{1},\:{a}_{{n}} \:=\:\mathrm{0} \\ $$$$\left(\mathrm{because}\:{f}\:\mathrm{is}\:\mathrm{odd}\right) \\ $$$$\:\forall{n}\in\mathbb{N}^{\ast} ,\:{b}_{\mathrm{2}{n}} \:=\:\mathrm{0}\:\mathrm{and}\:\forall{n}\in\mathbb{N},\:{b}_{\mathrm{2}{n}+\mathrm{1}} \:=\:\mathrm{2} \\ $$

Answered by mathmax by abdo last updated on 27/Jul/21

f(x)=(((e^(2ix) +e^(−2ix) )/2)/((e^(ix) −e^(−ix) )/(2i)))=i×((e^(2ix) +e^(−2ix) )/(e^(ix) −e^(−ix) )) changement e^(ix) =z give f(x)=g(z)=i.((z^2 +z^(−2) )/(z−z^(−1) )) =i((z^3 +z^(−1) )/(z^2 −1))=i((z^4 +1)/(z^3 −z)) =i .((z(z^3 −z)+z^2 +1)/(z^3 −z))=iz +i((z^2 +1)/(z(z^2 −1))) ((z^2 +1)/(z(z−1)(z+1)))=(a/z)+(b/(z−1))+(c/(z+1)) a=−1,b=1 ,c=(2/2)=1 ⇒((z^2 +1)/(z(z−1)(z+1))) =−(1/z)+(1/(z−1))+(1/(z+1))=−(1/z)−(1/(1−z))+(1/(1+z)) ⇒g(z)=iz−(1/z)−Σ_(n=0) ^∞ z^n +Σ_(n=0) ^∞ (−1)^n z^n =ie^(ix) −e^(−ix) +Σ_(n=0) ^∞ {(−1)^n −1}e^(inx) =i(cosx+isinx)−(cosx−isinx)+Σ_(n=0) ^∞ {(−1)^n −1}(cos(nx)+isin(nx)) =−sinx−cosx+i(cosx+sinx)+Σ_(n=0) ^∞ {(−1)^n −1}cos(nx)+iΣ(...) f(x)is real ⇒ f(x)=−sinx−cosx+Σ_(n=0) ^∞ {(−1)^n −1}cos(nx) f(x)=−sinx−cosx−2Σ_(n=0) ^∞ cos(2n+1)x

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\frac{\mathrm{e}^{\mathrm{2ix}} +\mathrm{e}^{−\mathrm{2ix}} }{\mathrm{2}}}{\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}}=\mathrm{i}×\frac{\mathrm{e}^{\mathrm{2ix}} +\mathrm{e}^{−\mathrm{2ix}} }{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }\:\mathrm{changement}\:\mathrm{e}^{\mathrm{ix}} \:=\mathrm{z}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{z}\right)=\mathrm{i}.\frac{\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}^{−\mathrm{2}} }{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }\:=\mathrm{i}\frac{\mathrm{z}^{\mathrm{3}} +\mathrm{z}^{−\mathrm{1}} }{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}=\mathrm{i}\frac{\mathrm{z}^{\mathrm{4}} +\mathrm{1}}{\mathrm{z}^{\mathrm{3}} −\mathrm{z}} \\ $$$$=\mathrm{i}\:.\frac{\mathrm{z}\left(\mathrm{z}^{\mathrm{3}} −\mathrm{z}\right)+\mathrm{z}^{\mathrm{2}} +\mathrm{1}}{\mathrm{z}^{\mathrm{3}} −\mathrm{z}}=\mathrm{iz}\:+\mathrm{i}\frac{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{z}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\frac{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{z}\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{z}+\mathrm{1}\right)}=\frac{\mathrm{a}}{\mathrm{z}}+\frac{\mathrm{b}}{\mathrm{z}−\mathrm{1}}+\frac{\mathrm{c}}{\mathrm{z}+\mathrm{1}} \\ $$$$\mathrm{a}=−\mathrm{1},\mathrm{b}=\mathrm{1}\:\:,\mathrm{c}=\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1}\:\Rightarrow\frac{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{z}\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{z}+\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{z}}+\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{z}+\mathrm{1}}=−\frac{\mathrm{1}}{\mathrm{z}}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{z}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{z}} \\ $$$$\Rightarrow\mathrm{g}\left(\mathrm{z}\right)=\mathrm{iz}−\frac{\mathrm{1}}{\mathrm{z}}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{n}} \:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{z}^{\mathrm{n}} \\ $$$$=\mathrm{ie}^{\mathrm{ix}} \:−\mathrm{e}^{−\mathrm{ix}} \:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left\{\left(−\mathrm{1}\right)^{\mathrm{n}} −\mathrm{1}\right\}\mathrm{e}^{\mathrm{inx}} \\ $$$$=\mathrm{i}\left(\mathrm{cosx}+\mathrm{isinx}\right)−\left(\mathrm{cosx}−\mathrm{isinx}\right)+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left\{\left(−\mathrm{1}\right)^{\mathrm{n}} −\mathrm{1}\right\}\left(\mathrm{cos}\left(\mathrm{nx}\right)+\mathrm{isin}\left(\mathrm{nx}\right)\right) \\ $$$$=−\mathrm{sinx}−\mathrm{cosx}+\mathrm{i}\left(\mathrm{cosx}+\mathrm{sinx}\right)+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left\{\left(−\mathrm{1}\right)^{\mathrm{n}} −\mathrm{1}\right\}\mathrm{cos}\left(\mathrm{nx}\right)+\mathrm{i}\Sigma\left(...\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\mathrm{is}\:\mathrm{real}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{sinx}−\mathrm{cosx}+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left\{\left(−\mathrm{1}\right)^{\mathrm{n}} −\mathrm{1}\right\}\mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{sinx}−\mathrm{cosx}−\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{x} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com