Question Number 148416 by mathdanisur last updated on 27/Jul/21

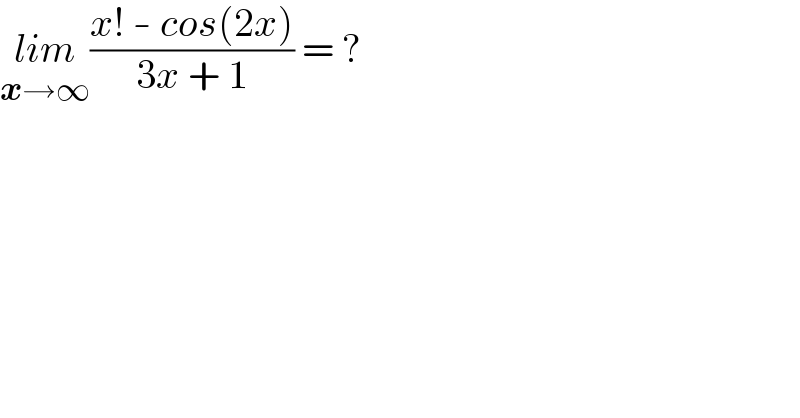
lim_(x→∞) ((x! - cos(2x))/(3x + 1)) = ?

Answered by mathmax by abdo last updated on 28/Jul/21

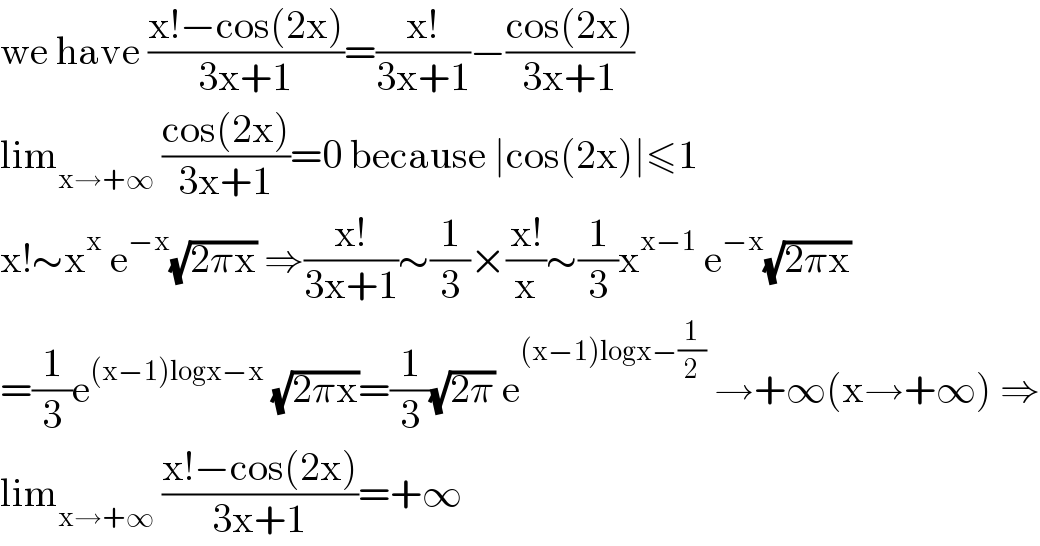
we have ((x!−cos(2x))/(3x+1))=((x!)/(3x+1))−((cos(2x))/(3x+1)) lim_(x→+∞) ((cos(2x))/(3x+1))=0 because ∣cos(2x)∣≤1 x!∼x^x e^(−x) (√(2πx)) ⇒((x!)/(3x+1))∼(1/3)×((x!)/x)∼(1/3)x^(x−1) e^(−x) (√(2πx)) =(1/3)e^((x−1)logx−x) (√(2πx))=(1/3)(√(2π)) e^((x−1)logx−(1/2)) →+∞(x→+∞) ⇒ lim_(x→+∞) ((x!−cos(2x))/(3x+1))=+∞

Commented bymathdanisur last updated on 28/Jul/21

Thankyoy Ser