Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 148466 by Ar Brandon last updated on 28/Jul/21

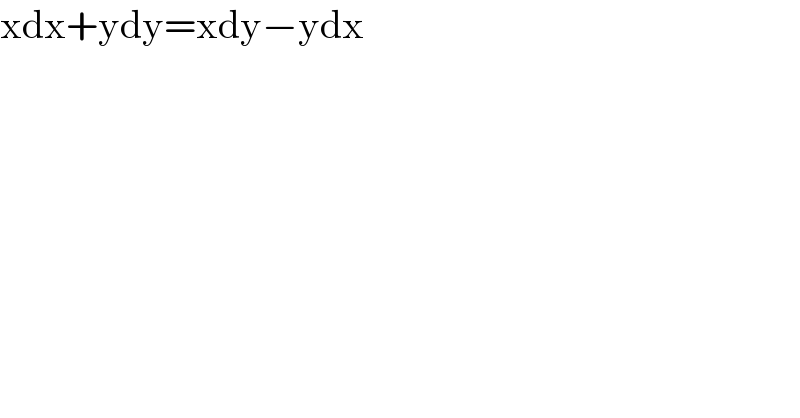
xdx+ydy=xdy−ydx

$$\mathrm{xdx}+\mathrm{ydy}=\mathrm{xdy}−\mathrm{ydx} \\ $$

Answered by bramlexs22 last updated on 28/Jul/21

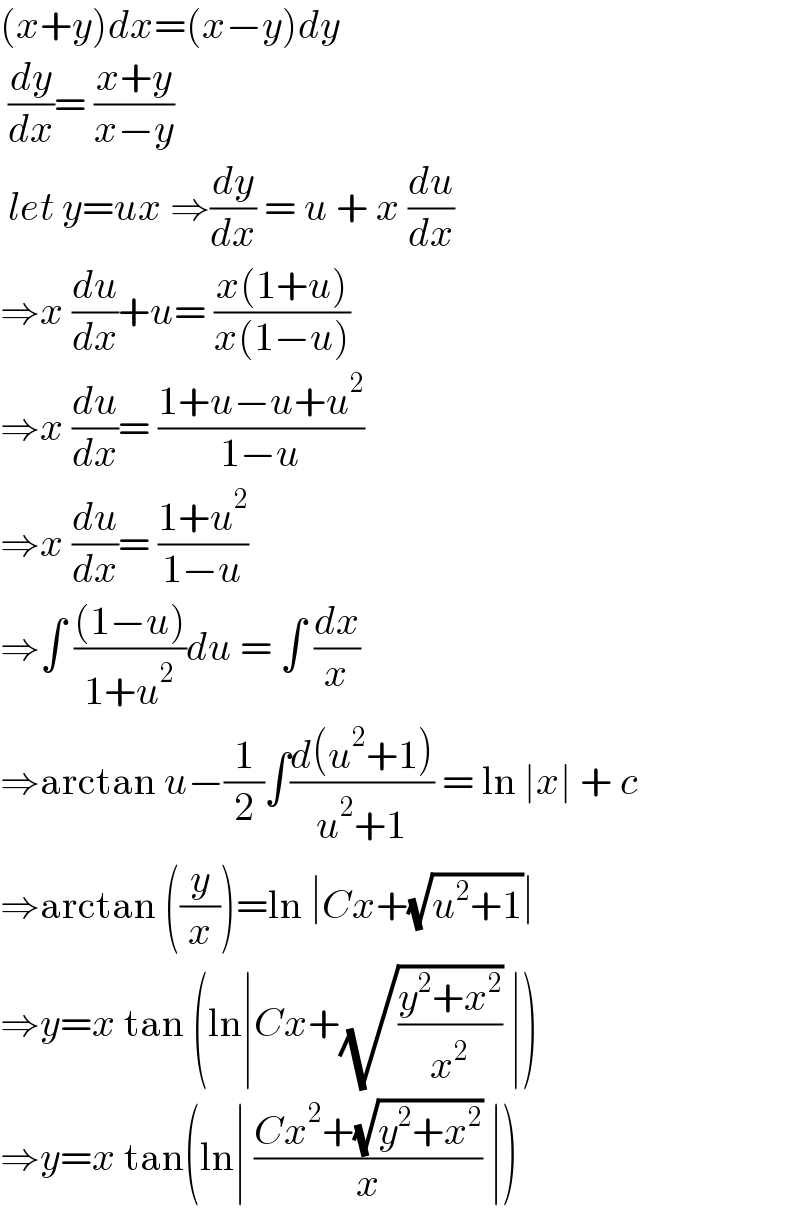
(x+y)dx=(x−y)dy (dy/dx)= ((x+y)/(x−y)) let y=ux ⇒(dy/dx) = u + x (du/dx) ⇒x (du/dx)+u= ((x(1+u))/(x(1−u))) ⇒x (du/dx)= ((1+u−u+u^2 )/(1−u)) ⇒x (du/dx)= ((1+u^2 )/(1−u)) ⇒∫ (((1−u))/(1+u^2 ))du = ∫ (dx/x) ⇒arctan u−(1/2)∫((d(u^2 +1))/(u^2 +1)) = ln ∣x∣ + c ⇒arctan ((y/x))=ln ∣Cx+(√(u^2 +1))∣ ⇒y=x tan (ln∣Cx+(√((y^2 +x^2 )/x^2 )) ∣) ⇒y=x tan(ln∣ ((Cx^2 +(√(y^2 +x^2 )))/x) ∣)

$$\left({x}+{y}\right){dx}=\left({x}−{y}\right){dy} \\ $$$$\:\frac{{dy}}{{dx}}=\:\frac{{x}+{y}}{{x}−{y}} \\ $$$$\:{let}\:{y}={ux}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:{u}\:+\:{x}\:\frac{{du}}{{dx}} \\ $$$$\Rightarrow{x}\:\frac{{du}}{{dx}}+{u}=\:\frac{{x}\left(\mathrm{1}+{u}\right)}{{x}\left(\mathrm{1}−{u}\right)} \\ $$$$\Rightarrow{x}\:\frac{{du}}{{dx}}=\:\frac{\mathrm{1}+{u}−{u}+{u}^{\mathrm{2}} }{\mathrm{1}−{u}} \\ $$$$\Rightarrow{x}\:\frac{{du}}{{dx}}=\:\frac{\mathrm{1}+{u}^{\mathrm{2}} }{\mathrm{1}−{u}} \\ $$$$\Rightarrow\int\:\frac{\left(\mathrm{1}−{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:=\:\int\:\frac{{dx}}{{x}} \\ $$$$\Rightarrow\mathrm{arctan}\:{u}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{{u}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{ln}\:\mid{x}\mid\:+\:{c} \\ $$$$\Rightarrow\mathrm{arctan}\:\left(\frac{{y}}{{x}}\right)=\mathrm{ln}\:\mid{Cx}+\sqrt{{u}^{\mathrm{2}} +\mathrm{1}}\mid \\ $$$$\Rightarrow{y}={x}\:\mathrm{tan}\:\left(\mathrm{ln}\mid{Cx}+\sqrt{\frac{{y}^{\mathrm{2}} +{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\:\mid\right) \\ $$$$\Rightarrow{y}={x}\:\mathrm{tan}\left(\mathrm{ln}\mid\:\frac{{Cx}^{\mathrm{2}} +\sqrt{{y}^{\mathrm{2}} +{x}^{\mathrm{2}} }}{{x}}\:\mid\right) \\ $$

Commented by Ar Brandon last updated on 28/Jul/21

Thanks for your method

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{method} \\ $$

Commented by Ar Brandon last updated on 28/Jul/21

⇒y=x tan(ln ∣((Cx^2 +(√(y^2 +x^2 )))/x) ∣)

$$\Rightarrow{y}={x}\:\mathrm{tan}\left(\mathrm{ln}\:\mid\frac{{Cx}^{\mathrm{2}} +\sqrt{{y}^{\mathrm{2}} +{x}^{\mathrm{2}} }}{{x}}\:\mid\right) \\ $$

Answered by Ar Brandon last updated on 28/Jul/21

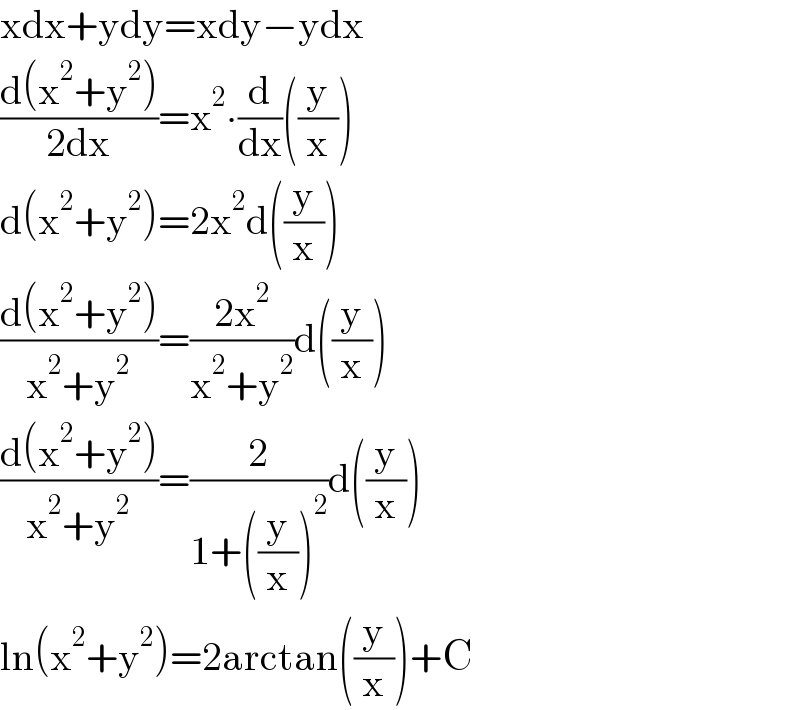
xdx+ydy=xdy−ydx ((d(x^2 +y^2 ))/(2dx))=x^2 ∙(d/dx)((y/x)) d(x^2 +y^2 )=2x^2 d((y/x)) ((d(x^2 +y^2 ))/(x^2 +y^2 ))=((2x^2 )/(x^2 +y^2 ))d((y/x)) ((d(x^2 +y^2 ))/(x^2 +y^2 ))=(2/(1+((y/x))^2 ))d((y/x)) ln(x^2 +y^2 )=2arctan((y/x))+C

$$\mathrm{xdx}+\mathrm{ydy}=\mathrm{xdy}−\mathrm{ydx} \\ $$$$\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{2dx}}=\mathrm{x}^{\mathrm{2}} \centerdot\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)=\mathrm{2x}^{\mathrm{2}} \mathrm{d}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\mathrm{d}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{1}+\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{2}} }\mathrm{d}\left(\frac{\mathrm{y}}{\mathrm{x}}\right) \\ $$$$\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)=\mathrm{2arctan}\left(\frac{\mathrm{y}}{\mathrm{x}}\right)+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com