
Question Number 96302 by mathmax by abdo last updated on 31/May/20
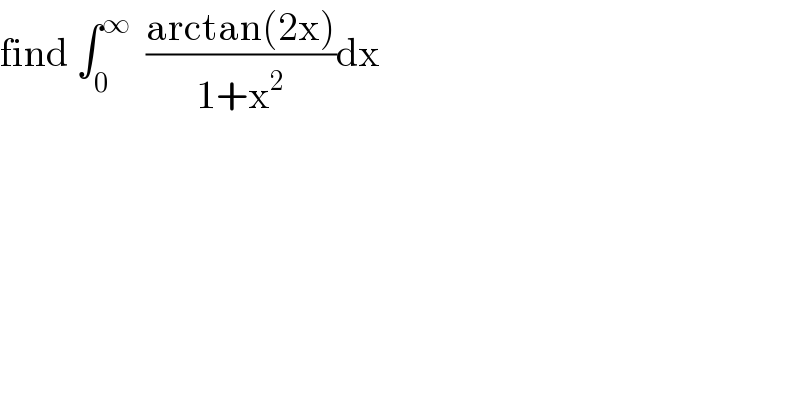
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}\left(\mathrm{2x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$
| ||
Question Number 96302 by mathmax by abdo last updated on 31/May/20 | ||
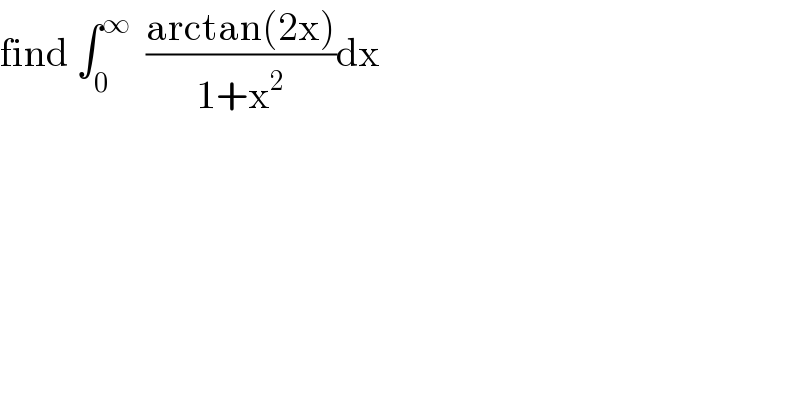 | ||
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}\left(\mathrm{2x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$ | ||