Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 148546 by mathdanisur last updated on 29/Jul/21

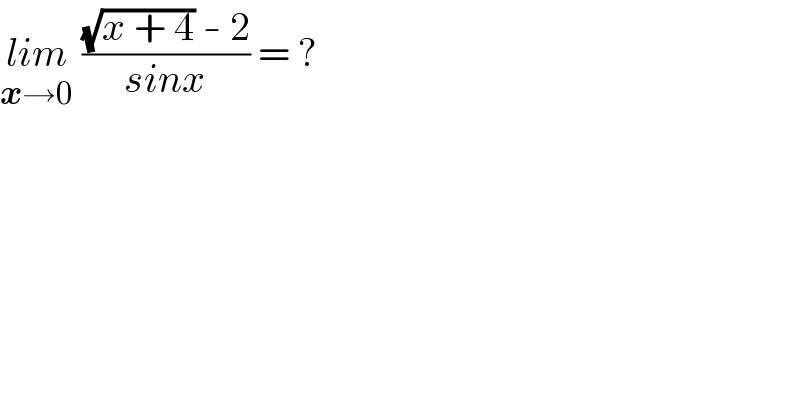
lim_(x→0) (((√(x + 4)) - 2)/(sinx)) = ?

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {{lim}}\:\frac{\sqrt{{x}\:+\:\mathrm{4}}\:-\:\mathrm{2}}{{sinx}}\:=\:? \\ $$

Commented by EDWIN88 last updated on 29/Jul/21

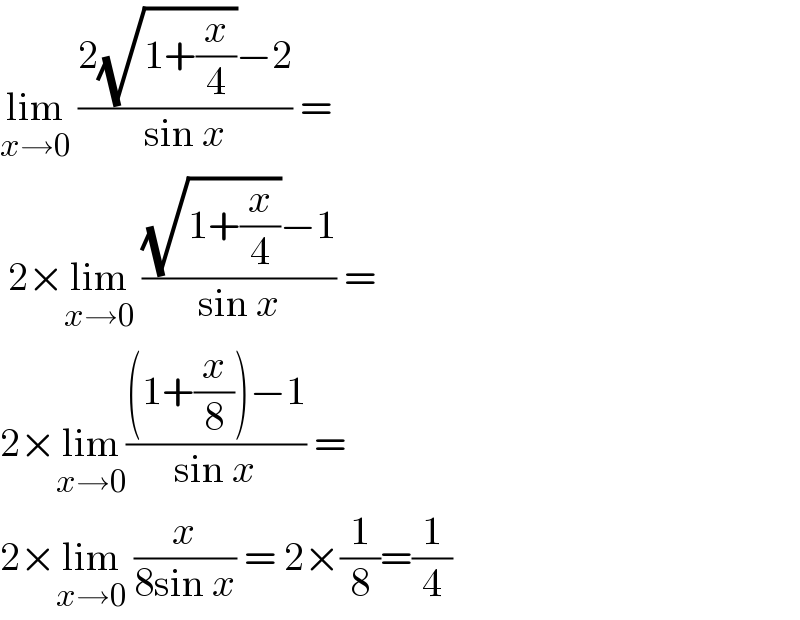
lim_(x→0) ((2(√(1+(x/4)))−2)/(sin x)) = 2×lim_(x→0) (((√(1+(x/4)))−1)/(sin x)) = 2×lim_(x→0) (((1+(x/8))−1)/(sin x)) = 2×lim_(x→0) (x/(8sin x)) = 2×(1/8)=(1/4)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\sqrt{\mathrm{1}+\frac{{x}}{\mathrm{4}}}−\mathrm{2}}{\mathrm{sin}\:{x}}\:= \\ $$$$\:\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\frac{{x}}{\mathrm{4}}}−\mathrm{1}}{\mathrm{sin}\:{x}}\:= \\ $$$$\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\frac{{x}}{\mathrm{8}}\right)−\mathrm{1}}{\mathrm{sin}\:{x}}\:= \\ $$$$\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}}{\mathrm{8sin}\:{x}}\:=\:\mathrm{2}×\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by mathdanisur last updated on 31/Jul/21

Thank you Ser

$${Thank}\:{you}\:{Ser} \\ $$

Answered by Olaf_Thorendsen last updated on 29/Jul/21

(((√(x+4))−2)/(sinx)) = ((2(√(1+(x/4)))−2)/(sinx)) ∼_0 ((2(1+(1/2)((x/4)))−2)/x) →_0 (1/4)

$$\frac{\sqrt{{x}+\mathrm{4}}−\mathrm{2}}{\mathrm{sin}{x}}\:=\:\:\frac{\mathrm{2}\sqrt{\mathrm{1}+\frac{{x}}{\mathrm{4}}}−\mathrm{2}}{\mathrm{sin}{x}} \\ $$$$\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}}{\mathrm{4}}\right)\right)−\mathrm{2}}{{x}}\:\underset{\mathrm{0}} {\rightarrow}\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by mathdanisur last updated on 29/Jul/21

Thank you Ser

$${Thank}\:{you}\:{Ser} \\ $$

Answered by hknkrc46 last updated on 29/Jul/21

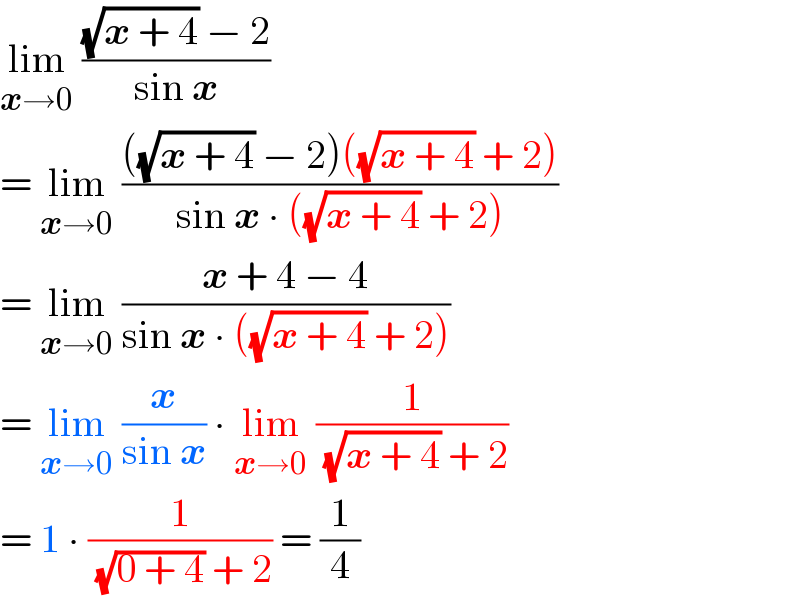
lim_(x→0) (((√(x + 4)) − 2)/(sin x)) = lim_(x→0) ((((√(x + 4)) − 2)((√(x + 4)) + 2))/(sin x ∙ ((√(x + 4)) + 2))) = lim_(x→0) ((x + 4 − 4)/(sin x ∙ ((√(x + 4)) + 2))) = lim_(x→0) (x/(sin x)) ∙ lim_(x→0) (1/( (√(x + 4)) + 2)) = 1 ∙ (1/( (√(0 + 4)) + 2)) = (1/4)

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\boldsymbol{{x}}\:+\:\mathrm{4}}\:−\:\mathrm{2}}{\mathrm{sin}\:\boldsymbol{{x}}}\: \\ $$$$=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\sqrt{\boldsymbol{{x}}\:+\:\mathrm{4}}\:−\:\mathrm{2}\right)\left(\sqrt{\boldsymbol{{x}}\:+\:\mathrm{4}}\:+\:\mathrm{2}\right)}{\mathrm{sin}\:\boldsymbol{{x}}\:\centerdot\:\left(\sqrt{\boldsymbol{{x}}\:+\:\mathrm{4}}\:+\:\mathrm{2}\right)} \\ $$$$=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}\:+\:\mathrm{4}\:−\:\mathrm{4}}{\mathrm{sin}\:\boldsymbol{{x}}\:\centerdot\:\left(\sqrt{\boldsymbol{{x}}\:+\:\mathrm{4}}\:+\:\mathrm{2}\right)} \\ $$$$=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\boldsymbol{{x}}}{\mathrm{sin}\:\boldsymbol{{x}}}\:\centerdot\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}\:+\:\mathrm{4}}\:+\:\mathrm{2}} \\ $$$$=\:\mathrm{1}\:\centerdot\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{0}\:+\:\mathrm{4}}\:+\:\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Commented by mathdanisur last updated on 29/Jul/21

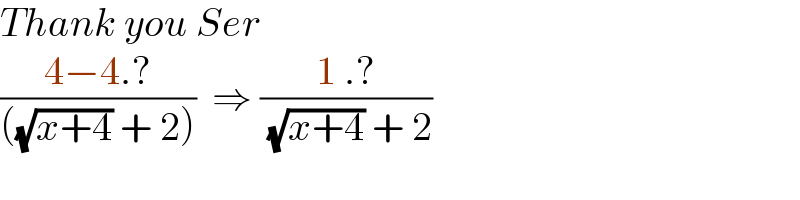
Thank you Ser ((4−4.?)/(((√(x+4)) + 2))) ⇒ ((1 .?)/( (√(x+4)) + 2))

$${Thank}\:{you}\:{Ser} \\ $$$$\frac{\mathrm{4}−\mathrm{4}.?}{\left(\sqrt{{x}+\mathrm{4}}\:+\:\mathrm{2}\right)}\:\:\Rightarrow\:\frac{\mathrm{1}\:.?}{\:\sqrt{{x}+\mathrm{4}}\:+\:\mathrm{2}} \\ $$

Answered by puissant last updated on 29/Jul/21

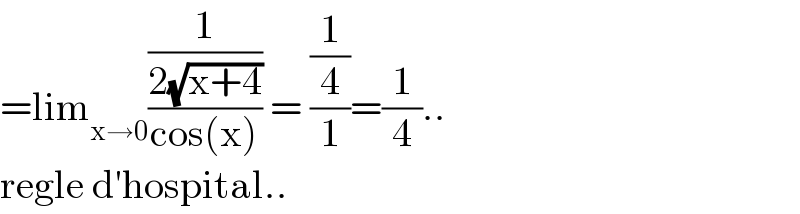
=lim_(x→0) ((1/(2(√(x+4))))/(cos(x))) = ((1/4)/1)=(1/4).. regle d′hospital..

$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{4}}}}{\mathrm{cos}\left(\mathrm{x}\right)}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{4}}.. \\ $$$$\mathrm{regle}\:\mathrm{d}'\mathrm{hospital}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com