
Previous in Relation and Functions Next in Relation and Functions
Question Number 148558 by puissant last updated on 29/Jul/21

$$\mathrm{Trouver}\:\mathrm{toutes}\:\mathrm{les}\:\mathrm{fonctions}\:\mathrm{continues} \\ $$$$\mathrm{f}:\mathbb{R}\rightarrow\mathbb{R}\:\mathrm{verifiant}: \\ $$$$\forall\left(\mathrm{x},\mathrm{y}\right)\in\mathbb{R}^{\mathrm{2}} ,\:\mathrm{f}\left(\mathrm{x}+\mathrm{y}\right)\mathrm{f}\left(\mathrm{x}−\mathrm{y}\right)=\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{f}^{\mathrm{2}} \left(\mathrm{y}\right).. \\ $$$$\mathrm{monsieur}\:\mathrm{j}'\mathrm{ai}\:\mathrm{suppos}\acute {\mathrm{e}}\:\mathrm{que}\:\mathrm{f}\:\mathrm{est}\:\mathrm{un}\: \\ $$$$\mathrm{morphisme}\:\mathrm{mutiplicatif}\:\mathrm{de}\:\mathbb{R}..\:\mathrm{mais}\:\mathrm{ca}\:\mathrm{ne} \\ $$$$\mathrm{sort}\:\mathrm{pas}... \\ $$
Answered by Olaf_Thorendsen last updated on 29/Jul/21
![∀(x,y)∈R^2 , f(x+y)f(x−y) = f^2 (x)f^2 (y) • On elimine d′emblee le cas trivial de la fonction identiquement nulle (1) • En particulier, pour x = y = 0 : f(0+0)f(0−0) = f^2 (0)f^2 (0) Et donc f(0) = 0 ou ±1. • ∀x∈R et pour y = 0 : f(x+0)f(x−0) = f^2 (x)f^2 (0) f^2 (x+0) = f^2 (x)f^2 (0) On elimine alors le cas f(0) = 0 avec (1). Et donc f(0) = ±1. ∀(x,y)∈R^2 , f(x+y)f(x−y) = f^2 (x)f^2 (y) Vu cette relation, et notamment les carres a droite, on voit que f est de signe constant. Dans toute la suite, on cherche des fonctions f strictement positives avec f(0) = 1. En posant g(x) = lnf(x), il vient : ∀(x,y)∈R^2 , g(x+y)+g(x−y) = 2[g(x)+g(y)] Mon intuition est alors de poser g(x) = wx^2 et l′on voit que cette famille de fonctions verifie l′equation. La famille de fonctions definies par f(x) = e^(ωx^2 ) verifie donc l′equation initiale. Apres, il reste a demontrer qu′il n′y en a pas d′autres. Mais on voit que si f est solution alors toute fonction h definie par h(x) = e^(ωx^2 ) f(x) est encore solution. La famille de fonctions {e^(ωx^2 ) } est donc generatrice de l′espace des solutions.](Q148591.png)
$$\forall\left({x},\mathrm{y}\right)\in\mathbb{R}^{\mathrm{2}} ,\:{f}\left({x}+{y}\right){f}\left({x}−{y}\right)\:=\:{f}^{\mathrm{2}} \left({x}\right){f}^{\mathrm{2}} \left({y}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{On}\:\mathrm{elimine}\:\mathrm{d}'\mathrm{emblee}\:\mathrm{le}\:\mathrm{cas}\:\mathrm{trivial} \\ $$$$\mathrm{de}\:\mathrm{la}\:\mathrm{fonction}\:\mathrm{identiquement}\:\mathrm{nulle}\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{En}\:\mathrm{particulier},\:\mathrm{pour}\:{x}\:=\:{y}\:=\:\mathrm{0}\:: \\ $$$${f}\left(\mathrm{0}+\mathrm{0}\right){f}\left(\mathrm{0}−\mathrm{0}\right)\:=\:{f}^{\mathrm{2}} \left(\mathrm{0}\right){f}^{\mathrm{2}} \left(\mathrm{0}\right) \\ $$$$\mathrm{Et}\:\mathrm{donc}\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{0}\:\mathrm{ou}\:\pm\mathrm{1}. \\ $$$$\: \\ $$$$\bullet\:\forall{x}\in\mathbb{R}\:\mathrm{et}\:\mathrm{pour}\:{y}\:=\:\mathrm{0}\:: \\ $$$${f}\left({x}+\mathrm{0}\right){f}\left({x}−\mathrm{0}\right)\:=\:{f}^{\mathrm{2}} \left({x}\right){f}^{\mathrm{2}} \left(\mathrm{0}\right) \\ $$$${f}^{\mathrm{2}} \left({x}+\mathrm{0}\right)\:=\:{f}^{\mathrm{2}} \left({x}\right){f}^{\mathrm{2}} \left(\mathrm{0}\right) \\ $$$$\mathrm{On}\:\mathrm{elimine}\:\mathrm{alors}\:\mathrm{le}\:\mathrm{cas}\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{0}\:\mathrm{avec}\:\left(\mathrm{1}\right). \\ $$$$\mathrm{Et}\:\mathrm{donc}\:{f}\left(\mathrm{0}\right)\:=\:\pm\mathrm{1}. \\ $$$$ \\ $$$$\forall\left({x},\mathrm{y}\right)\in\mathbb{R}^{\mathrm{2}} ,\:{f}\left({x}+{y}\right){f}\left({x}−{y}\right)\:=\:{f}^{\mathrm{2}} \left({x}\right){f}^{\mathrm{2}} \left({y}\right) \\ $$$$\mathrm{Vu}\:\mathrm{cette}\:\mathrm{relation},\:\mathrm{et}\:\mathrm{notamment}\:\mathrm{les} \\ $$$$\mathrm{carres}\:\mathrm{a}\:\mathrm{droite},\:\mathrm{on}\:\mathrm{voit}\:\mathrm{que}\:{f}\:\mathrm{est}\:\mathrm{de} \\ $$$$\mathrm{signe}\:\mathrm{constant}.\:\mathrm{Dans}\:\mathrm{toute}\:\mathrm{la}\:\mathrm{suite}, \\ $$$$\mathrm{on}\:\mathrm{cherche}\:\mathrm{des}\:\mathrm{fonctions}\:{f}\:\mathrm{strictement} \\ $$$$\mathrm{positives}\:\mathrm{avec}\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{1}. \\ $$$$ \\ $$$$\mathrm{En}\:\mathrm{posant}\:{g}\left({x}\right)\:=\:\mathrm{ln}{f}\left({x}\right),\:\mathrm{il}\:\mathrm{vient}\:: \\ $$$$\forall\left({x},\mathrm{y}\right)\in\mathbb{R}^{\mathrm{2}} ,\:{g}\left({x}+{y}\right)+{g}\left({x}−{y}\right)\:=\:\mathrm{2}\left[{g}\left({x}\right)+{g}\left({y}\right)\right] \\ $$$$ \\ $$$$\mathrm{Mon}\:\mathrm{intuition}\:\mathrm{est}\:\mathrm{alors}\:\mathrm{de}\:\mathrm{poser} \\ $$$${g}\left({x}\right)\:=\:{wx}^{\mathrm{2}} \:\mathrm{et}\:\mathrm{l}'\mathrm{on}\:\mathrm{voit}\:\mathrm{que}\:\mathrm{cette} \\ $$$$\mathrm{famille}\:\mathrm{de}\:\mathrm{fonctions}\:\mathrm{verifie}\:\mathrm{l}'\mathrm{equation}. \\ $$$$ \\ $$$$\mathrm{La}\:\mathrm{famille}\:\mathrm{de}\:\mathrm{fonctions}\:\mathrm{definies}\:\mathrm{par} \\ $$$${f}\left({x}\right)\:=\:{e}^{\omega{x}^{\mathrm{2}} } \:\mathrm{verifie}\:\mathrm{donc}\:\mathrm{l}'\mathrm{equation} \\ $$$$\mathrm{initiale}. \\ $$$$\mathrm{Apres},\:\mathrm{il}\:\mathrm{reste}\:\mathrm{a}\:\mathrm{demontrer}\:\mathrm{qu}'\mathrm{il}\:\mathrm{n}'\mathrm{y}\:\mathrm{en} \\ $$$$\mathrm{a}\:\mathrm{pas}\:\mathrm{d}'\mathrm{autres}. \\ $$$$\mathrm{Mais}\:\mathrm{on}\:\mathrm{voit}\:\mathrm{que}\:\mathrm{si}\:{f}\:\mathrm{est}\:\mathrm{solution}\:\mathrm{alors} \\ $$$$\mathrm{toute}\:\mathrm{fonction}\:{h}\:\mathrm{definie}\:\mathrm{par} \\ $$$${h}\left({x}\right)\:=\:{e}^{\omega{x}^{\mathrm{2}} } {f}\left({x}\right)\:\mathrm{est}\:\mathrm{encore}\:\mathrm{solution}. \\ $$$$\mathrm{La}\:\mathrm{famille}\:\mathrm{de}\:\mathrm{fonctions}\:\left\{{e}^{\omega{x}^{\mathrm{2}} } \right\}\:\mathrm{est}\:\mathrm{donc} \\ $$$$\mathrm{generatrice}\:\mathrm{de}\:\mathrm{l}'\mathrm{espace}\:\mathrm{des}\:\mathrm{solutions}. \\ $$
Answered by Kamel last updated on 29/Jul/21
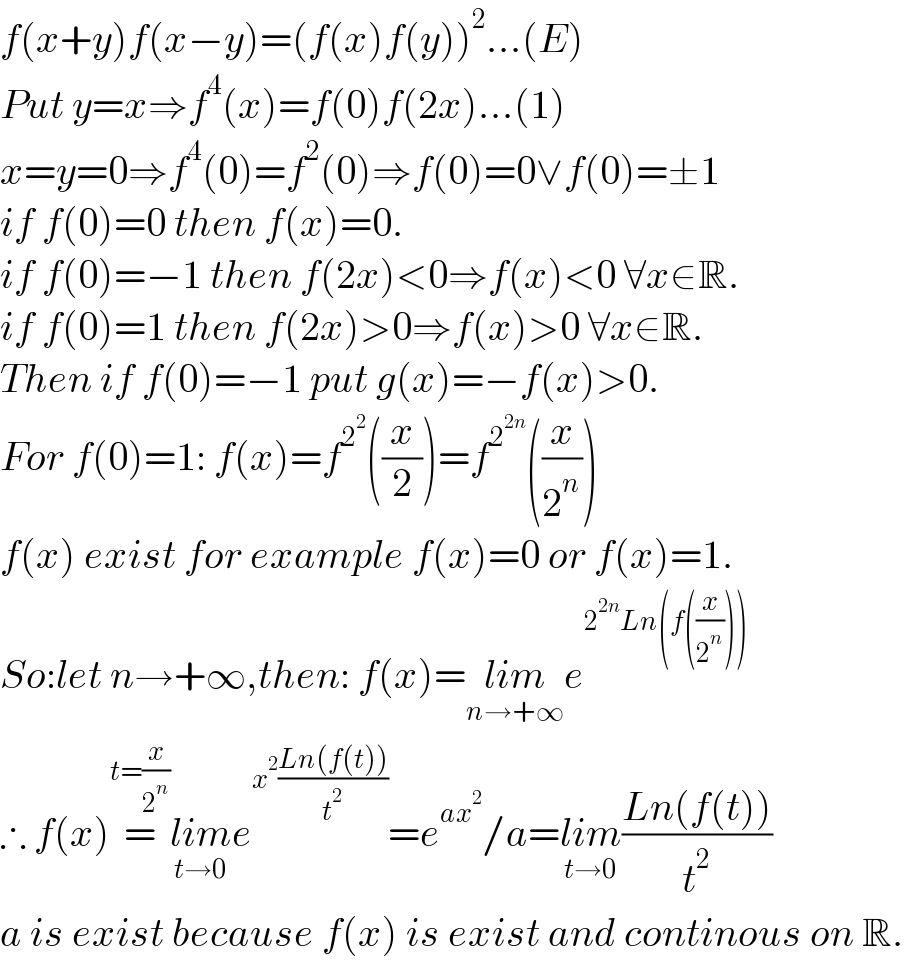
$${f}\left({x}+{y}\right){f}\left({x}−{y}\right)=\left({f}\left({x}\right){f}\left({y}\right)\right)^{\mathrm{2}} ...\left({E}\right) \\ $$$${Put}\:{y}={x}\Rightarrow{f}^{\mathrm{4}} \left({x}\right)={f}\left(\mathrm{0}\right){f}\left(\mathrm{2}{x}\right)...\left(\mathrm{1}\right) \\ $$$${x}={y}=\mathrm{0}\Rightarrow{f}^{\mathrm{4}} \left(\mathrm{0}\right)={f}^{\mathrm{2}} \left(\mathrm{0}\right)\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{0}\vee{f}\left(\mathrm{0}\right)=\pm\mathrm{1} \\ $$$${if}\:{f}\left(\mathrm{0}\right)=\mathrm{0}\:{then}\:{f}\left({x}\right)=\mathrm{0}. \\ $$$${if}\:{f}\left(\mathrm{0}\right)=−\mathrm{1}\:{then}\:{f}\left(\mathrm{2}{x}\right)<\mathrm{0}\Rightarrow{f}\left({x}\right)<\mathrm{0}\:\forall{x}\in\mathbb{R}. \\ $$$${if}\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:{then}\:{f}\left(\mathrm{2}{x}\right)>\mathrm{0}\Rightarrow{f}\left({x}\right)>\mathrm{0}\:\forall{x}\in\mathbb{R}. \\ $$$${Then}\:{if}\:{f}\left(\mathrm{0}\right)=−\mathrm{1}\:{put}\:{g}\left({x}\right)=−{f}\left({x}\right)>\mathrm{0}. \\ $$$${For}\:{f}\left(\mathrm{0}\right)=\mathrm{1}:\:{f}\left({x}\right)={f}^{\mathrm{2}^{\mathrm{2}} } \left(\frac{{x}}{\mathrm{2}}\right)={f}^{\mathrm{2}^{\mathrm{2}{n}} } \left(\frac{{x}}{\mathrm{2}^{{n}} }\right) \\ $$$${f}\left({x}\right)\:{exist}\:{for}\:{example}\:{f}\left({x}\right)=\mathrm{0}\:{or}\:{f}\left({x}\right)=\mathrm{1}. \\ $$$${So}:{let}\:{n}\rightarrow+\infty,{then}:\:{f}\left({x}\right)=\underset{{n}\rightarrow+\infty} {{lim}e}^{\mathrm{2}^{\mathrm{2}{n}} {Ln}\left({f}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\right)} \\ $$$$\therefore\:{f}\left({x}\right)\overset{{t}=\frac{{x}}{\mathrm{2}^{{n}} }} {=}\underset{{t}\rightarrow\mathrm{0}} {{lim}e}^{{x}^{\mathrm{2}} \frac{{Ln}\left({f}\left({t}\right)\right)}{{t}^{\mathrm{2}} }} ={e}^{{ax}^{\mathrm{2}} } /{a}=\underset{{t}\rightarrow\mathrm{0}} {{lim}}\frac{{Ln}\left({f}\left({t}\right)\right)}{{t}^{\mathrm{2}} } \\ $$$${a}\:{is}\:{exist}\:{because}\:{f}\left({x}\right)\:{is}\:{exist}\:{and}\:{continous}\:{on}\:\mathbb{R}. \\ $$
Commented by puissant last updated on 29/Jul/21

$$\mathrm{thanks}.. \\ $$
