Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 148565 by mathmax by abdo last updated on 29/Jul/21

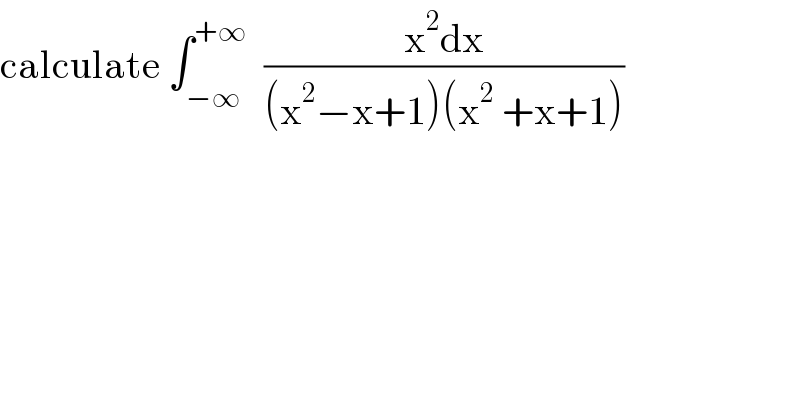
$$\mathrm{calculate}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\mathrm{x}}^2\mathrm{dx}}{({\mathrm{x}}^2-\mathrm{x}+1)({\mathrm{x}}^2+\mathrm{x}+1)}$$

Answered by Ar Brandon last updated on 29/Jul/21

$$\mathrm{{\rm Y}}={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{x^{2}dx}{(x^2-x+1)(x^2+x+1)}=2{\int }_0^{\mathrm{\infty }}\frac{x^{2}dx}{(x^2-x+1)(x^2+x+1)}$$$$=2{\int }_0^1\frac{x^{2}dx}{(x^2-x+1)(x^2+x+1)}+2{\int }_1^{\mathrm{\infty }}\frac{x^{2}dx}{(x^2-x+1)(x^2+x+1)}$$$$=2{\int }_0^1\frac{x^{2}dx}{(x^2-x+1)(x^2+x+1)}+2{\int }_0^1\frac{dx}{(x^2-x+1)(x^2+x+1)}$$$$=2{\int }_0^1\frac{x^2+1}{(x^2-x+1)(x^2+x+1)}dx=2{\int }_0^1\frac{x^2+1}{x^4+x^2+1}dx$$$$=2{\int }_0^1\frac{1+\frac{1}{x^2}}{x^2+1+\frac{1}{x^2}}dx=2{\int }_0^1\frac{1+\frac{1}{x^2}}{{(x-\frac{1}{x})}^2+3}dx$$$$=2{\int }_0^1\frac{d(x-\frac{1}{x})}{{(x-\frac{1}{x})}^2+3}=\frac{2}{\sqrt{3}}{\left[\arctan \left(\frac{x^2-1}{\sqrt{3}x}\right)\right]}_0^1=\frac{\pi }{\sqrt{3}}$$

Answered by mathmax by abdo last updated on 29/Jul/21

$$\mathrm{\Psi }={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{{\mathrm{x}}^2}{({\mathrm{x}}^2-\mathrm{x}+1)({\mathrm{x}}^2+\mathrm{x}+1)}\mathrm{dx}\mathrm{let}\mathrm{\Lambda }\left(\mathrm{z}\right)=\frac{{\mathrm{z}}^2}{({\mathrm{z}}^2-\mathrm{z}+1)({\mathrm{z}}^2+\mathrm{z}+1)}$$$$\mathrm{poles}\mathrm{of}\mathrm{\Lambda }?$$$${\mathrm{z}}^2-\mathrm{z}+1=0\to \mathrm{\Delta }=-3\Rightarrow {\mathrm{z}}_1=\frac{1+\mathrm{i}\sqrt{3}}{2}={\mathrm{e}}^{\frac{\mathrm{i}\pi }{3}}\mathrm{and}{\mathrm{z}}_2=\frac{1-\mathrm{i}\sqrt{3}}{2}={\mathrm{e}}^{-\frac{\mathrm{i}\pi }{3}}$$$${\mathrm{z}}^2+\mathrm{z}+1=0\to \mathrm{\Delta }=-3\Rightarrow {\mathrm{x}}_1=\frac{-1+\mathrm{i}\sqrt{3}}{2}={\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}\Rightarrow {\mathrm{x}}_2={\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}}\Rightarrow$$$$\mathrm{\Lambda }\left(\mathrm{z}\right)=\frac{{\mathrm{z}}^2}{(\mathrm{z}-{\mathrm{e}}^{\frac{\mathrm{i}\pi }{3}})(\mathrm{z}-{\mathrm{e}}^{-\frac{\mathrm{i}\pi }{3}})(\mathrm{z}-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})(\mathrm{z}-{\mathrm{e}}^{-\frac{2\mathrm{i}\pi }{3}})}$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\mathrm{\Lambda }\left(\mathrm{z}\right)\mathrm{dz}=2\mathrm{i}\pi \{\mathrm{Res}(\mathrm{\Lambda },{\mathrm{e}}^{\frac{\mathrm{i}\pi }{3}})+\mathrm{Res}(\mathrm{\Lambda },{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})\}$$$$\mathrm{Res}(\mathrm{\Lambda },{\mathrm{e}}^{\frac{\mathrm{i}\pi }{3}})=\frac{{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{2\mathrm{isin}\left(\frac{\pi }{3}\right)\times }\frac{({\mathrm{e}}^{\frac{\mathrm{i}\pi }{3}}-1)}{{\mathrm{e}}^{\mathrm{i}\pi }-1}$$$$=\frac{1}{-4\mathrm{i}\times \frac{\sqrt{3}}{2}}(-1-{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})=\frac{1+{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}}{2\mathrm{i}\sqrt{3}}$$$$\mathrm{Res}(\mathrm{\Lambda },{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}})=\frac{{\mathrm{e}}^{\frac{4\mathrm{i}\pi }{3}}}{2\mathrm{isin}\left(\frac{2\pi }{3}\right)}\times \frac{{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}+1}{2}$$$$=\frac{1+{\mathrm{e}}^{\frac{4\mathrm{i}\pi }{3}}}{4\mathrm{i}\times \frac{\sqrt{3}}{2}}=\frac{1+{\mathrm{e}}^{\frac{4\mathrm{i}\pi }{3}}}{2\mathrm{i}\sqrt{3}}\Rightarrow$$$${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\mathrm{\Lambda }\left(\mathrm{z}\right)\mathrm{dz}=\frac{2\mathrm{i}\pi }{2\mathrm{i}\sqrt{3}}\{1+{\mathrm{e}}^{\frac{2\mathrm{i}\pi }{3}}+1-{\mathrm{e}}^{\frac{\mathrm{i}\pi }{3}}\}$$$$=\frac{\pi }{\sqrt{3}}\{2-\frac{1}{2}+\frac{\mathrm{i}\sqrt{3}}{2}-\frac{1}{2}-\mathrm{i}\frac{\sqrt{3}}{2}\}=\frac{\pi }{\sqrt{3}}\Rightarrow \mathrm{\Psi }=\frac{\pi }{\sqrt{3}}.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com