Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 148568 by mathmax by abdo last updated on 29/Jul/21

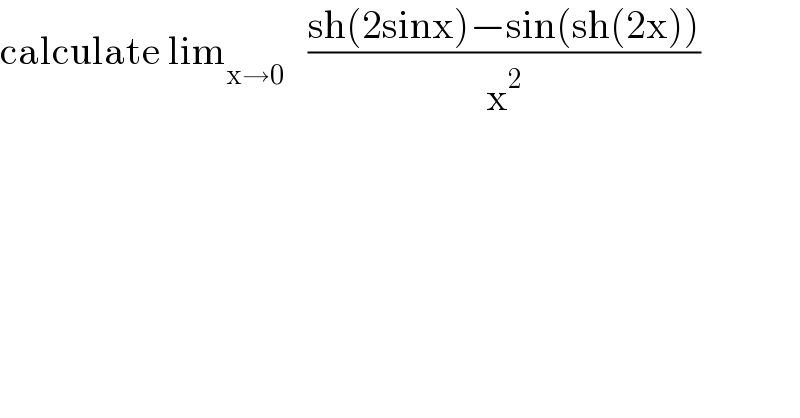
calculate lim_(x→0) ((sh(2sinx)−sin(sh(2x)))/x^2 )

$$\mathrm{calculate}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{sh}\left(\mathrm{2sinx}\right)−\mathrm{sin}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$

Answered by Ar Brandon last updated on 29/Jul/21

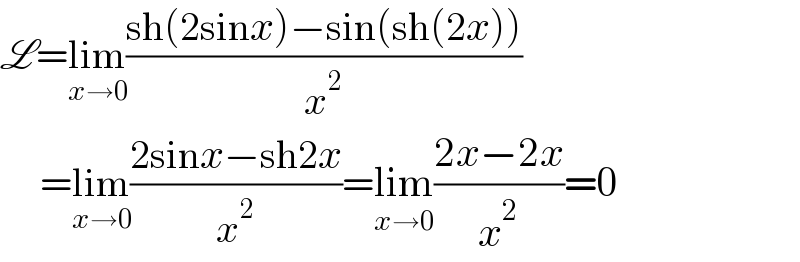
L=lim_(x→0) ((sh(2sinx)−sin(sh(2x)))/x^2 ) =lim_(x→0) ((2sinx−sh2x)/x^2 )=lim_(x→0) ((2x−2x)/x^2 )=0

$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sh}\left(\mathrm{2sin}{x}\right)−\mathrm{sin}\left(\mathrm{sh}\left(\mathrm{2}{x}\right)\right)}{{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}{x}−\mathrm{sh2}{x}}{{x}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}{x}−\mathrm{2}{x}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$

Answered by mathmax by abdo last updated on 29/Jul/21

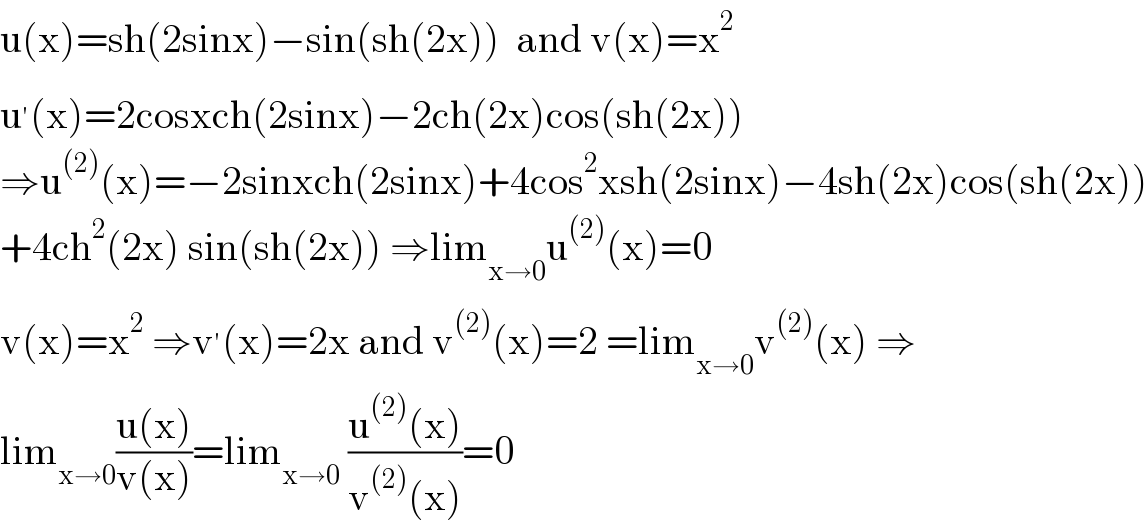
u(x)=sh(2sinx)−sin(sh(2x)) and v(x)=x^2 u^′ (x)=2cosxch(2sinx)−2ch(2x)cos(sh(2x)) ⇒u^((2)) (x)=−2sinxch(2sinx)+4cos^2 xsh(2sinx)−4sh(2x)cos(sh(2x)) +4ch^2 (2x) sin(sh(2x)) ⇒lim_(x→0) u^((2)) (x)=0 v(x)=x^2 ⇒v^′ (x)=2x and v^((2)) (x)=2 =lim_(x→0) v^((2)) (x) ⇒ lim_(x→0) ((u(x))/(v(x)))=lim_(x→0) ((u^((2)) (x))/(v^((2)) (x)))=0

$$\mathrm{u}\left(\mathrm{x}\right)=\mathrm{sh}\left(\mathrm{2sinx}\right)−\mathrm{sin}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)\:\:\mathrm{and}\:\mathrm{v}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{u}^{'} \left(\mathrm{x}\right)=\mathrm{2cosxch}\left(\mathrm{2sinx}\right)−\mathrm{2ch}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right) \\ $$$$\Rightarrow\mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=−\mathrm{2sinxch}\left(\mathrm{2sinx}\right)+\mathrm{4cos}^{\mathrm{2}} \mathrm{xsh}\left(\mathrm{2sinx}\right)−\mathrm{4sh}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right) \\ $$$$+\mathrm{4ch}^{\mathrm{2}} \left(\mathrm{2x}\right)\:\mathrm{sin}\left(\mathrm{sh}\left(\mathrm{2x}\right)\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\mathrm{v}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \:\Rightarrow\mathrm{v}^{'} \left(\mathrm{x}\right)=\mathrm{2x}\:\mathrm{and}\:\mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\mathrm{2}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\mathrm{u}\left(\mathrm{x}\right)}{\mathrm{v}\left(\mathrm{x}\right)}=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)}{\mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)}=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com