Question Number 148570 by mathmax by abdo last updated on 29/Jul/21

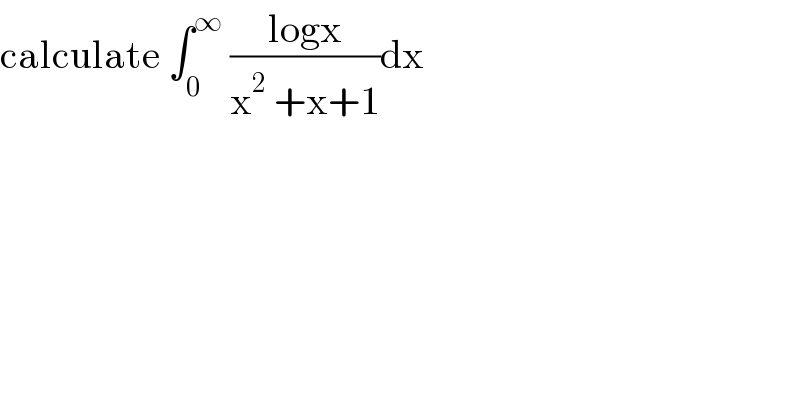
calculate ∫_0 ^∞ ((logx)/(x^2 +x+1))dx

Answered by Ar Brandon last updated on 29/Jul/21

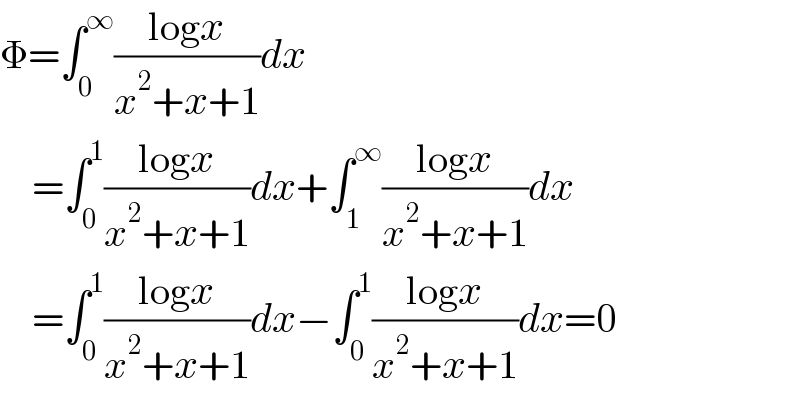
Φ=∫_0 ^∞ ((logx)/(x^2 +x+1))dx =∫_0 ^1 ((logx)/(x^2 +x+1))dx+∫_1 ^∞ ((logx)/(x^2 +x+1))dx =∫_0 ^1 ((logx)/(x^2 +x+1))dx−∫_0 ^1 ((logx)/(x^2 +x+1))dx=0

Answered by mathmax by abdo last updated on 29/Jul/21

∫_0 ^∞ ((logx)/(x^2 +x+1))dx =−(1/2)Re(Σ Res(f(z)log^2 z ,a_i ) f(z)=(1/(z^2 +z+1)) poles of f! Δ=1−4=−3 ⇒z_1 =((−1+i(√3))/2) =e^((2iπ)/3) and z_2 =((−1−i(√3))/2) ϕ(z)=f(z)log^2 z ⇒ϕ(z)=((log^2 z)/((z−z_1 )(z−z_2 ))) Res(ϕ,e^((2iπ)/3) ) =(((((2iπ)/3))^2 )/(i(√3))) =−((4π^2 )/(9(i(√3)))) =((4iπ^2 )/(9(√3))) Res(ϕ,e^(−((2iπ)/3)) )=(((−((2iπ)/3))^2 )/(−i(√3)))=((4π^2 )/(9(i(√3))))=((−4iπ^2 )/(9(√3))) ⇒ Σ Res(ϕ..)=0 ⇒∫_0 ^∞ ((logx)/(x^2 +x+1))dx=0