Question Number 148573 by mathdanisur last updated on 29/Jul/21

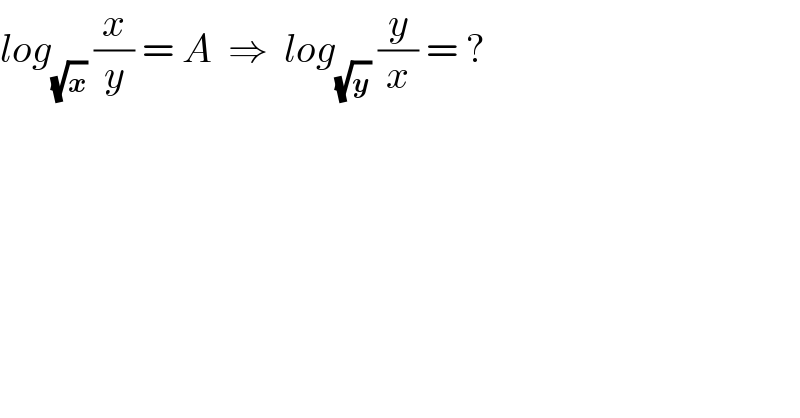
log_(√x) (x/y) = A ⇒ log_(√y) (y/x) = ?

Answered by Ar Brandon last updated on 29/Jul/21

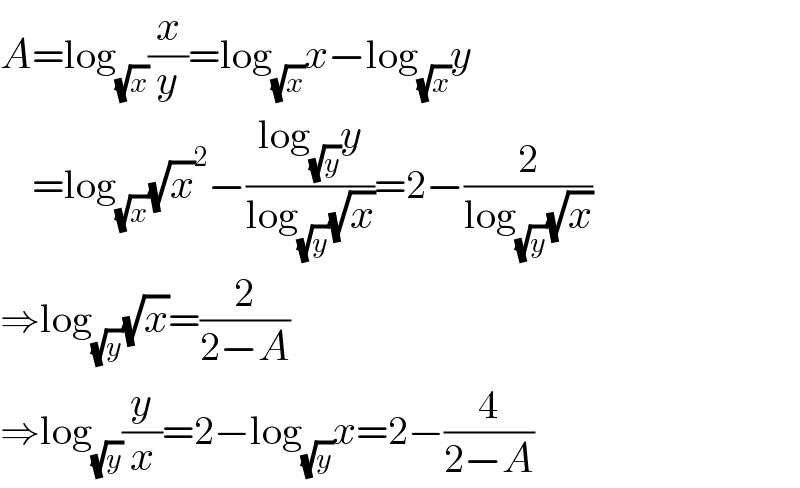
A=log_(√x) (x/y)=log_(√x) x−log_(√x) y =log_(√x) (√x) ^2 −((log_(√y) y)/(log_(√y) (√x)))=2−(2/(log_(√y) (√x))) ⇒log_(√y) (√x)=(2/(2−A)) ⇒log_(√y) (y/x)=2−log_(√y) x=2−(4/(2−A))

Commented bypuissant last updated on 29/Jul/21

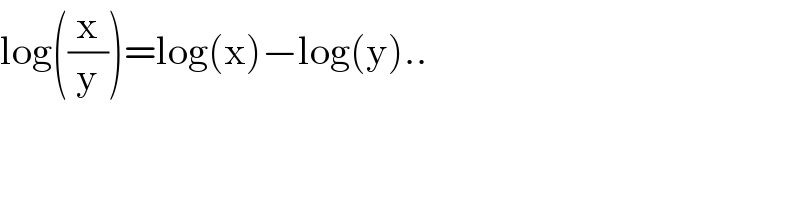
log((x/y))=log(x)−log(y)..

Commented byAr Brandon last updated on 29/Jul/21

Merci pour la remarque.

Commented bymathdanisur last updated on 29/Jul/21

Thank you Sir

Commented byAr Brandon last updated on 29/Jul/21

You′re welcome !

Answered by EDWIN88 last updated on 29/Jul/21

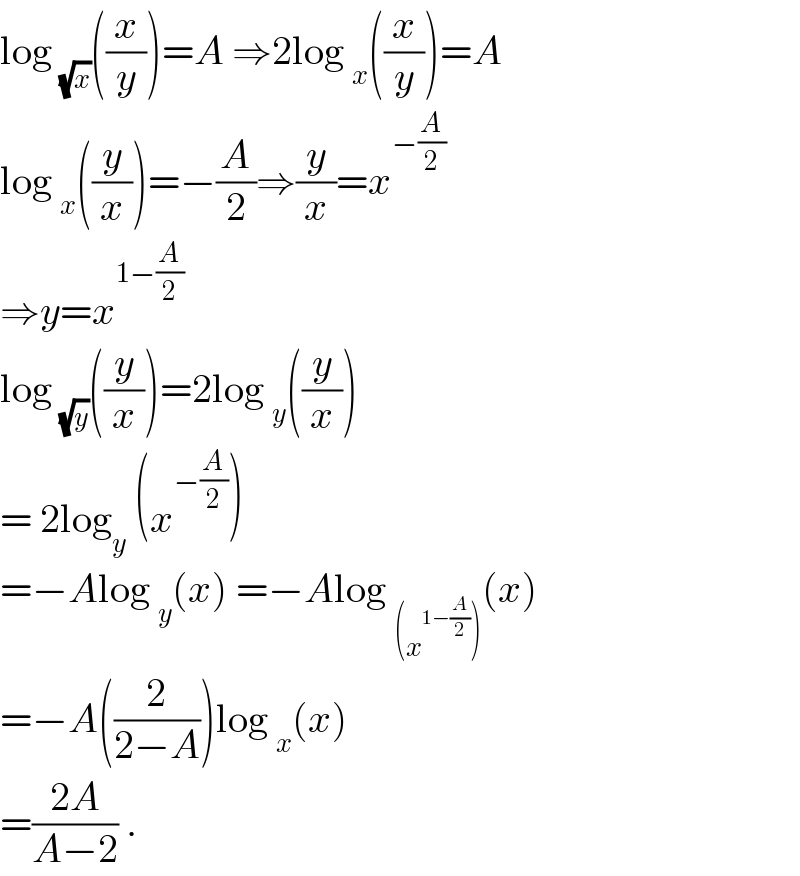
log _(√x) ((x/y))=A ⇒2log _x ((x/y))=A log _x ((y/x))=−(A/2)⇒(y/x)=x^(−(A/2)) ⇒y=x^(1−(A/2)) log _(√y) ((y/x))=2log _y ((y/x)) = 2log_y (x^(−(A/2)) ) =−Alog _y (x) =−Alog _((x^(1−(A/2)) )) (x) =−A((2/(2−A)))log _x (x) =((2A)/(A−2)) .

Commented bymathdanisur last updated on 29/Jul/21

Thank you Ser