Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148609 by learner001 last updated on 29/Jul/21

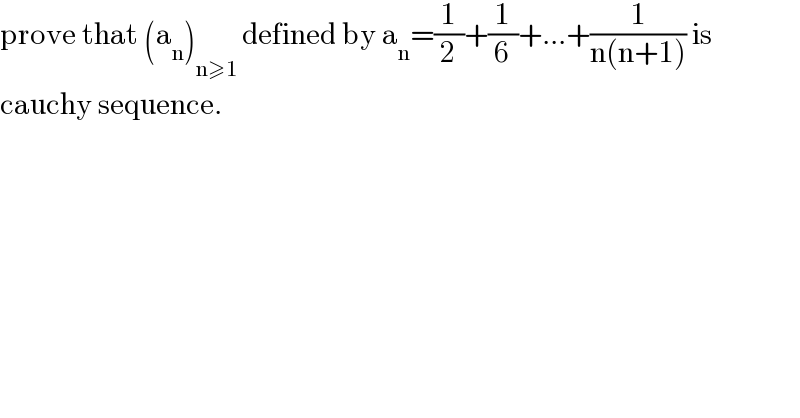
prove that (a_n )_(n≥1 ) defined by a_n =(1/2)+(1/6)+...+(1/(n(n+1))) is cauchy sequence.

$$\mathrm{prove}\:\mathrm{that}\:\left(\mathrm{a}_{\mathrm{n}} \right)_{\mathrm{n}\geqslant\mathrm{1}\:} \mathrm{defined}\:\mathrm{by}\:\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+...+\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}\:\mathrm{is}\: \\ $$$$\mathrm{cauchy}\:\mathrm{sequence}. \\ $$

Commented by learner001 last updated on 29/Jul/21

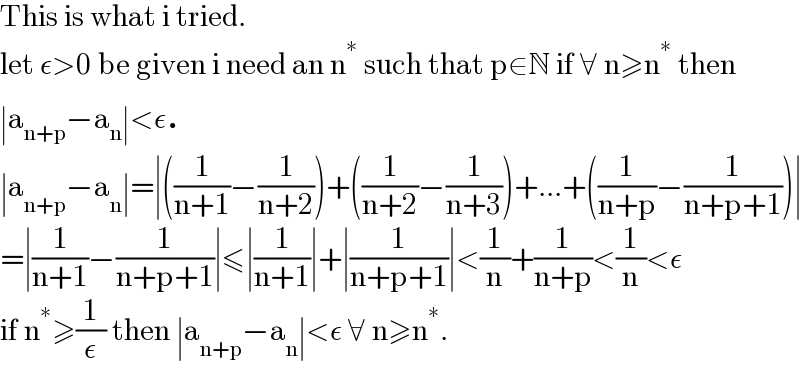
This is what i tried. let ε>0 be given i need an n^∗ such that p∈N if ∀ n≥n^∗ then ∣a_(n+p) −a_n ∣<ε. ∣a_(n+p) −a_n ∣=∣((1/(n+1))−(1/(n+2)))+((1/(n+2))−(1/(n+3)))+...+((1/(n+p))−(1/(n+p+1)))∣ =∣(1/(n+1))−(1/(n+p+1))∣≤∣(1/(n+1))∣+∣(1/(n+p+1))∣<(1/n)+(1/(n+p))<(1/n)<ε if n^∗ ≥(1/ε) then ∣a_(n+p) −a_n ∣<ε ∀ n≥n^∗ .

$$\mathrm{This}\:\mathrm{is}\:\mathrm{what}\:\mathrm{i}\:\mathrm{tried}. \\ $$$$\mathrm{let}\:\epsilon>\mathrm{0}\:\mathrm{be}\:\mathrm{given}\:\mathrm{i}\:\mathrm{need}\:\mathrm{an}\:\mathrm{n}^{\ast} \:\mathrm{such}\:\mathrm{that}\:\mathrm{p}\in\mathbb{N}\:\mathrm{if}\:\forall\:\mathrm{n}\geqslant\mathrm{n}^{\ast} \:\mathrm{then} \\ $$$$\mid\mathrm{a}_{\mathrm{n}+\mathrm{p}} −\mathrm{a}_{\mathrm{n}} \mid<\epsilon. \\ $$$$\mid\mathrm{a}_{\mathrm{n}+\mathrm{p}} −\mathrm{a}_{\mathrm{n}} \mid=\mid\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{3}}\right)+...+\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{p}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{p}+\mathrm{1}}\right)\mid \\ $$$$=\mid\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{p}+\mathrm{1}}\mid\leqslant\mid\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mid+\mid\frac{\mathrm{1}}{\mathrm{n}+\mathrm{p}+\mathrm{1}}\mid<\frac{\mathrm{1}}{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{p}}<\frac{\mathrm{1}}{\mathrm{n}}<\epsilon \\ $$$$\mathrm{if}\:\mathrm{n}^{\ast} \geqslant\frac{\mathrm{1}}{\epsilon}\:\mathrm{then}\:\mid\mathrm{a}_{\mathrm{n}+\mathrm{p}} −\mathrm{a}_{\mathrm{n}} \mid<\epsilon\:\forall\:\mathrm{n}\geqslant\mathrm{n}^{\ast} . \\ $$

Commented by learner001 last updated on 29/Jul/21

is this correct?

Terms of Service

Privacy Policy

Contact: info@tinkutara.com