
Question Number 14863 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17

Commented by adelson last updated on 05/Jun/17

$${what}'{s}\:\boldsymbol{{W}}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17
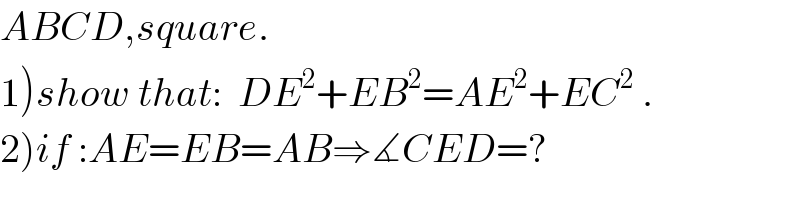
$${ABCD},{square}. \\ $$$$\left.\mathrm{1}\right){show}\:{that}:\:\:{DE}^{\mathrm{2}} +{EB}^{\mathrm{2}} ={AE}^{\mathrm{2}} +{EC}^{\mathrm{2}} \:. \\ $$$$\left.\mathrm{2}\right){if}\::{AE}={EB}={AB}\Rightarrow\measuredangle{CED}=? \\ $$
Commented by RasheedSoomro last updated on 05/Jun/17
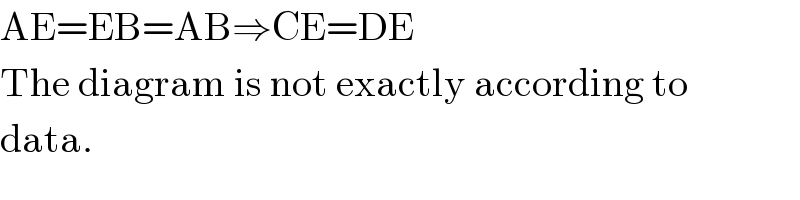
$$\mathrm{AE}=\mathrm{EB}=\mathrm{AB}\Rightarrow\mathrm{CE}=\mathrm{DE} \\ $$$$\mathrm{The}\:\mathrm{diagram}\:\mathrm{is}\:\mathrm{not}\:\mathrm{exactly}\:\mathrm{according}\:\mathrm{to} \\ $$$$\mathrm{data}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17

$${mr}\:{Rasheed}!\:{in}\:{part}\:#\mathrm{2},\:{we}\:{assume}\: \\ $$$${that}:\:{if}\:{AE}={EB}={AB}. \\ $$$${for}\:{part}\:#\mathrm{2}\:,{diagram}\:{not}\:{in}\:{scale}. \\ $$$${figure}\:{of}\:{mr}\:{Ajfour}\:{is}\:{correct}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17
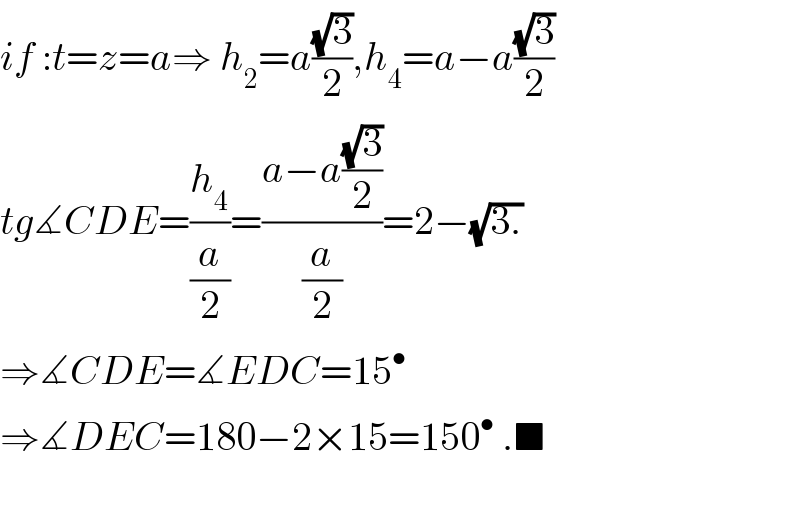
$${if}\::{t}={z}={a}\Rightarrow\:{h}_{\mathrm{2}} ={a}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}},{h}_{\mathrm{4}} ={a}−{a}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${tg}\measuredangle{CDE}=\frac{{h}_{\mathrm{4}} }{\frac{{a}}{\mathrm{2}}}=\frac{{a}−{a}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{{a}}{\mathrm{2}}}=\mathrm{2}−\sqrt{\mathrm{3}.} \\ $$$$\Rightarrow\measuredangle{CDE}=\measuredangle{EDC}=\mathrm{15}^{\bullet} \\ $$$$\Rightarrow\measuredangle{DEC}=\mathrm{180}−\mathrm{2}×\mathrm{15}=\mathrm{150}^{\bullet} \:.\blacksquare \\ $$$$ \\ $$
Answered by ajfour last updated on 05/Jun/17
![DE^2 +EB^2 =x^2 +y^2 +(a−x)^2 +(a−y)^2 AE^2 +EC^2 =(a−x)^2 +y^2 +x^2 +(a−y)^2 therefore equal. When △AEB is equilateral, a−y=y or y=(a/2) a−x= acos (π/6) = ((a(√3))/2) ⇒ x =a(1−((√3)/2)) = a(((2−(√3))/2)) ∠CED= 2tan^(−1) (((a−y)/x)) =2tan^(−1) ((y/x)) =2tan^(−1) [(((a/2))/(a(2−(√3))/2)))] =2tan^(−1) (2+(√3)) or ∠CED=π− tan^(−1) ((1/(√3))) =π−(π/6)=((5π)/6) .](Q14871.png)
$${DE}^{\mathrm{2}} +{EB}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left({a}−{x}\right)^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} \\ $$$${AE}^{\mathrm{2}} +{EC}^{\mathrm{2}} =\left({a}−{x}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}^{\mathrm{2}} +\left({a}−{y}\right)^{\mathrm{2}} \\ $$$${therefore}\:{equal}. \\ $$$$ \\ $$$${When}\:\bigtriangleup{AEB}\:{is}\:{equilateral}, \\ $$$$\:\:{a}−{y}={y}\:\:\:\:{or}\:\:\:\:{y}=\frac{{a}}{\mathrm{2}} \\ $$$$\:\:{a}−{x}=\:{a}\mathrm{cos}\:\frac{\pi}{\mathrm{6}}\:=\:\frac{{a}\sqrt{\mathrm{3}}}{\mathrm{2}}\: \\ $$$$\:\Rightarrow\:\:\:{x}\:={a}\left(\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:=\:{a}\left(\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\:\:\angle{CED}=\:\mathrm{2tan}^{−\mathrm{1}} \left(\frac{{a}−{y}}{{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2tan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2tan}^{−\mathrm{1}} \left[\frac{\left({a}/\mathrm{2}\right)}{\left.{a}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)/\mathrm{2}\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2tan}^{−\mathrm{1}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\:{or}\:\angle{CED}=\pi−\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\pi−\frac{\pi}{\mathrm{6}}=\frac{\mathrm{5}\pi}{\mathrm{6}}\:. \\ $$
Commented by ajfour last updated on 05/Jun/17

Commented by RasheedSoomro last updated on 05/Jun/17

$$\mathrm{You}'\mathrm{re}\:\mathrm{quicker}! \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17

$${thank}\:{you}\:{mr}\:{Ajfour}!{your}\:{answer}\:{is} \\ $$$${quick}\:{and}\:{nice}\:{and}\:{correct}\:{and}\:{smart}! \\ $$$${god}\:{bless}\:{you}\:{my}\:{friend}. \\ $$
Commented by ajfour last updated on 05/Jun/17

$${Tanks}\:{of}\:{thanks}\:{Sir}. \\ $$
