Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148631 by tabata last updated on 29/Jul/21

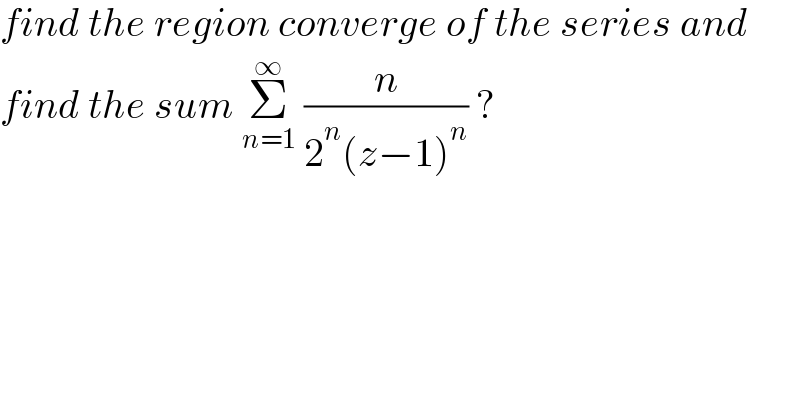
find the region converge of the series and find the sum Σ_(n=1) ^∞ (n/(2^n (z−1)^n )) ?

$${find}\:{the}\:{region}\:{converge}\:{of}\:{the}\:{series}\:{and}\: \\ $$$${find}\:{the}\:{sum}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{n}}{\mathrm{2}^{{n}} \left({z}−\mathrm{1}\right)^{{n}} }\:? \\ $$

Commented by tabata last updated on 29/Jul/21

????

$$???? \\ $$

Answered by mathmax by abdo last updated on 30/Jul/21

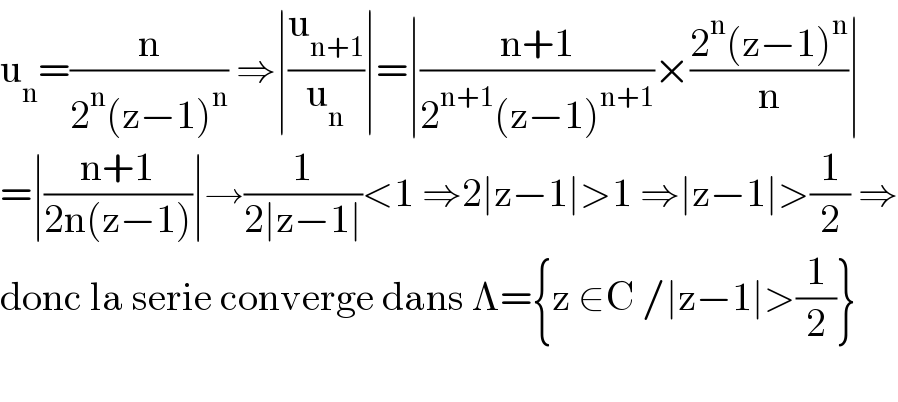
u_n =(n/(2^n (z−1)^n )) ⇒∣(u_(n+1) /u_n )∣=∣((n+1)/(2^(n+1) (z−1)^(n+1) ))×((2^n (z−1)^n )/n)∣ =∣((n+1)/(2n(z−1)))∣→(1/(2∣z−1∣))<1 ⇒2∣z−1∣>1 ⇒∣z−1∣>(1/2) ⇒ donc la serie converge dans Λ={z ∈C /∣z−1∣>(1/2)}

$$\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{n}}{\mathrm{2}^{\mathrm{n}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} }\:\Rightarrow\mid\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} }{\mathrm{u}_{\mathrm{n}} }\mid=\mid\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }×\frac{\mathrm{2}^{\mathrm{n}} \left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}\mid \\ $$$$=\mid\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2n}\left(\mathrm{z}−\mathrm{1}\right)}\mid\rightarrow\frac{\mathrm{1}}{\mathrm{2}\mid\mathrm{z}−\mathrm{1}\mid}<\mathrm{1}\:\Rightarrow\mathrm{2}\mid\mathrm{z}−\mathrm{1}\mid>\mathrm{1}\:\Rightarrow\mid\mathrm{z}−\mathrm{1}\mid>\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{donc}\:\mathrm{la}\:\mathrm{serie}\:\mathrm{converge}\:\mathrm{dans}\:\Lambda=\left\{\mathrm{z}\:\in\mathrm{C}\:/\mid\mathrm{z}−\mathrm{1}\mid>\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$$$ \\ $$

Commented by Sozan last updated on 30/Jul/21

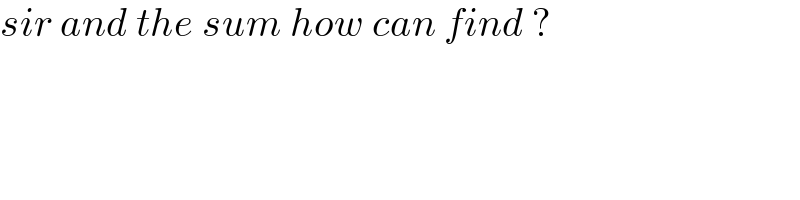
sir and the sum how can find ?

$${sir}\:{and}\:{the}\:{sum}\:{how}\:{can}\:{find}\:? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com