Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148635 by learner001 last updated on 29/Jul/21

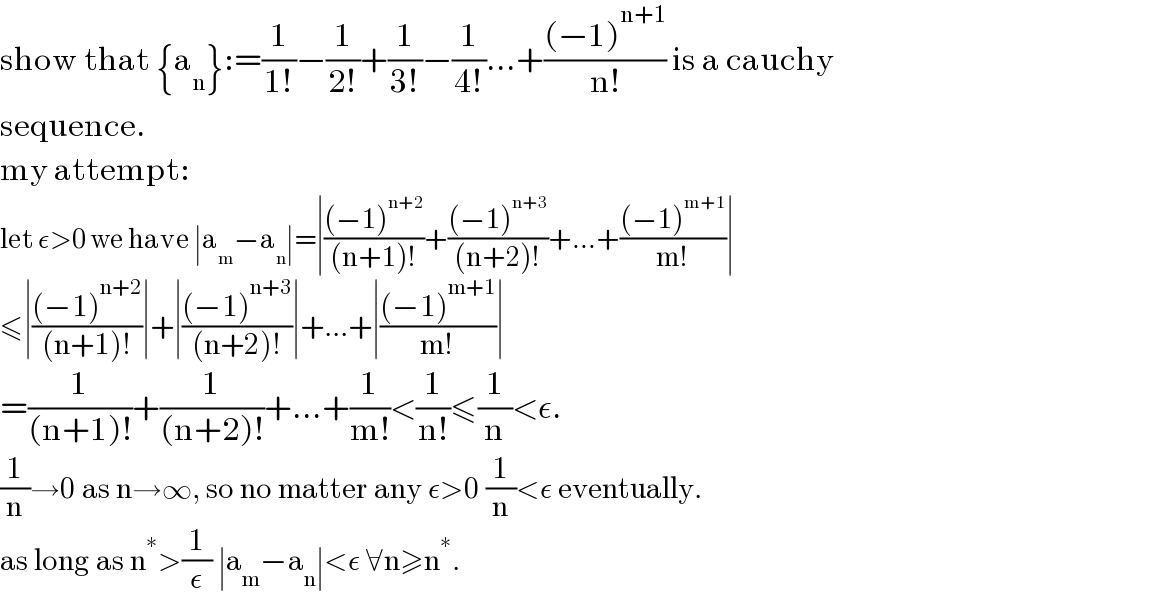
show that {a_n }:=(1/(1!))−(1/(2!))+(1/(3!))−(1/(4!))...+(((−1)^(n+1) )/(n!)) is a cauchy sequence. my attempt: let ε>0 we have ∣a_m −a_n ∣=∣(((−1)^(n+2) )/((n+1)!))+(((−1)^(n+3) )/((n+2)!))+...+(((−1)^(m+1) )/(m!))∣ ≤∣(((−1)^(n+2) )/((n+1)!))∣+∣(((−1)^(n+3) )/((n+2)!))∣+...+∣(((−1)^(m+1) )/(m!))∣ =(1/((n+1)!))+(1/((n+2)!))+...+(1/(m!))<(1/(n!))≤(1/n)<ε. (1/n)→0 as n→∞, so no matter any ε>0 (1/n)<ε eventually. as long as n^∗ >(1/ε) ∣a_m −a_n ∣<ε ∀n≥n^∗ .

$$\mathrm{show}\:\mathrm{that}\:\left\{\mathrm{a}_{\mathrm{n}} \right\}:=\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}...+\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}!}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cauchy} \\ $$ $$\mathrm{sequence}. \\ $$ $$\mathrm{my}\:\mathrm{attempt}: \\ $$ $$\mathrm{let}\:\epsilon>\mathrm{0}\:\mathrm{we}\:\mathrm{have}\:\mid\mathrm{a}_{\mathrm{m}} −\mathrm{a}_{\mathrm{n}} \mid=\mid\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}} }{\left(\mathrm{n}+\mathrm{1}\right)!}+\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{3}} }{\left(\mathrm{n}+\mathrm{2}\right)!}+...+\frac{\left(−\mathrm{1}\right)^{\mathrm{m}+\mathrm{1}} }{\mathrm{m}!}\mid \\ $$ $$\leqslant\mid\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{2}} }{\left(\mathrm{n}+\mathrm{1}\right)!}\mid+\mid\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{3}} }{\left(\mathrm{n}+\mathrm{2}\right)!}\mid+...+\mid\frac{\left(−\mathrm{1}\right)^{\mathrm{m}+\mathrm{1}} }{\mathrm{m}!}\mid \\ $$ $$=\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}+\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{2}\right)!}+...+\frac{\mathrm{1}}{\mathrm{m}!}<\frac{\mathrm{1}}{\mathrm{n}!}\leqslant\frac{\mathrm{1}}{\mathrm{n}}<\epsilon. \\ $$ $$\frac{\mathrm{1}}{\mathrm{n}}\rightarrow\mathrm{0}\:\mathrm{as}\:\mathrm{n}\rightarrow\infty,\:\mathrm{so}\:\mathrm{no}\:\mathrm{matter}\:\mathrm{any}\:\epsilon>\mathrm{0}\:\frac{\mathrm{1}}{\mathrm{n}}<\epsilon\:\mathrm{eventually}. \\ $$ $$\mathrm{as}\:\mathrm{long}\:\mathrm{as}\:\mathrm{n}^{\ast} >\frac{\mathrm{1}}{\epsilon}\:\mid\mathrm{a}_{\mathrm{m}} −\mathrm{a}_{\mathrm{n}} \mid<\epsilon\:\forall\mathrm{n}\geqslant\mathrm{n}^{\ast} .\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com