Question Number 148677 by nadovic last updated on 30/Jul/21

A series of natural numbers are grouped as 1+(2+3)+(4+5+6)+... such that the rth group contains r terms. Show that the sum of the numbers in the (2r−1)th group is r^4 −(r−1)^4 .

Answered by gsk2684 last updated on 30/Jul/21

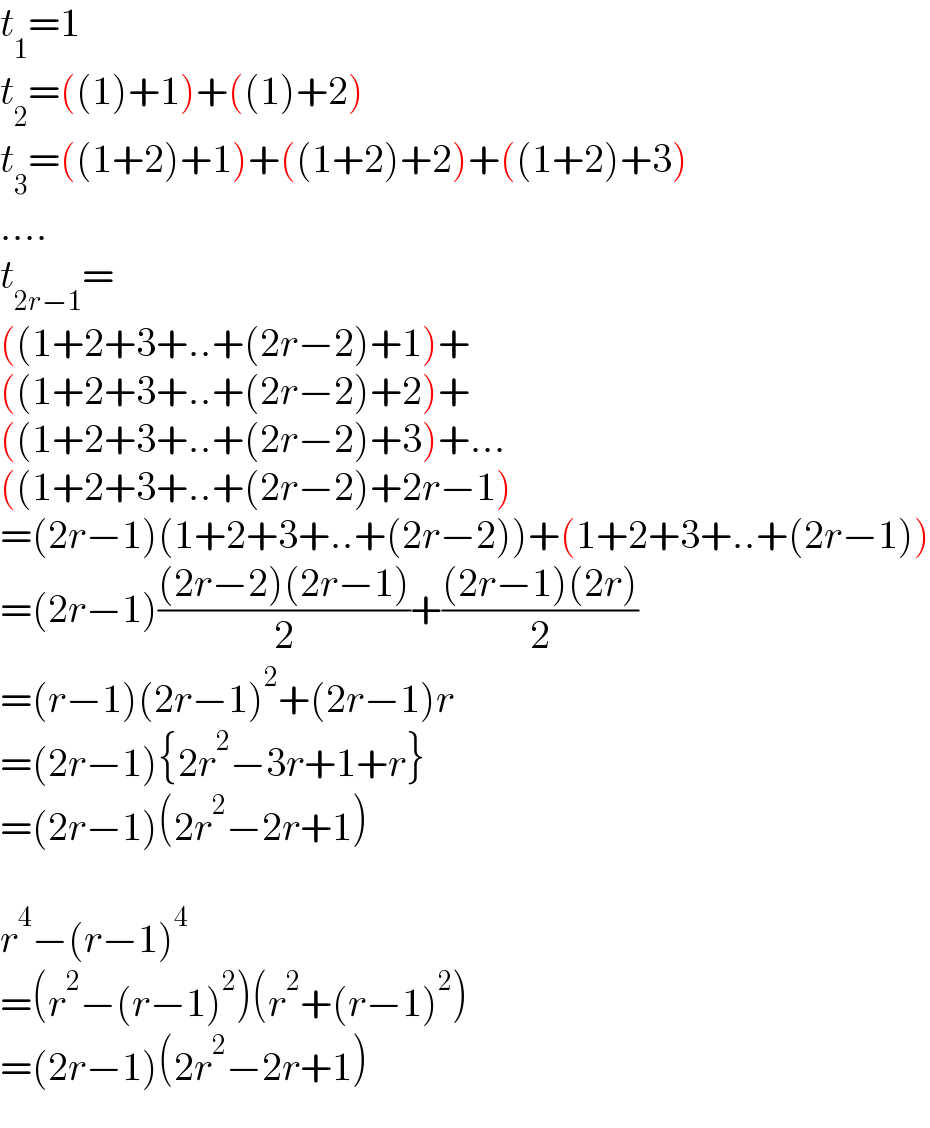
t_1 =1 t_2 =((1)+1)+((1)+2) t_3 =((1+2)+1)+((1+2)+2)+((1+2)+3) .... t_(2r−1) = ((1+2+3+..+(2r−2)+1)+ ((1+2+3+..+(2r−2)+2)+ ((1+2+3+..+(2r−2)+3)+... ((1+2+3+..+(2r−2)+2r−1) =(2r−1)(1+2+3+..+(2r−2))+(1+2+3+..+(2r−1)) =(2r−1)(((2r−2)(2r−1))/2)+(((2r−1)(2r))/2) =(r−1)(2r−1)^2 +(2r−1)r =(2r−1){2r^2 −3r+1+r} =(2r−1)(2r^2 −2r+1) r^4 −(r−1)^4 =(r^2 −(r−1)^2 )(r^2 +(r−1)^2 ) =(2r−1)(2r^2 −2r+1)

Commented bynadovic last updated on 30/Jul/21

Thank Sir