Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 148753 by Jonathanwaweh last updated on 30/Jul/21

Answered by mathmax by abdo last updated on 31/Jul/21

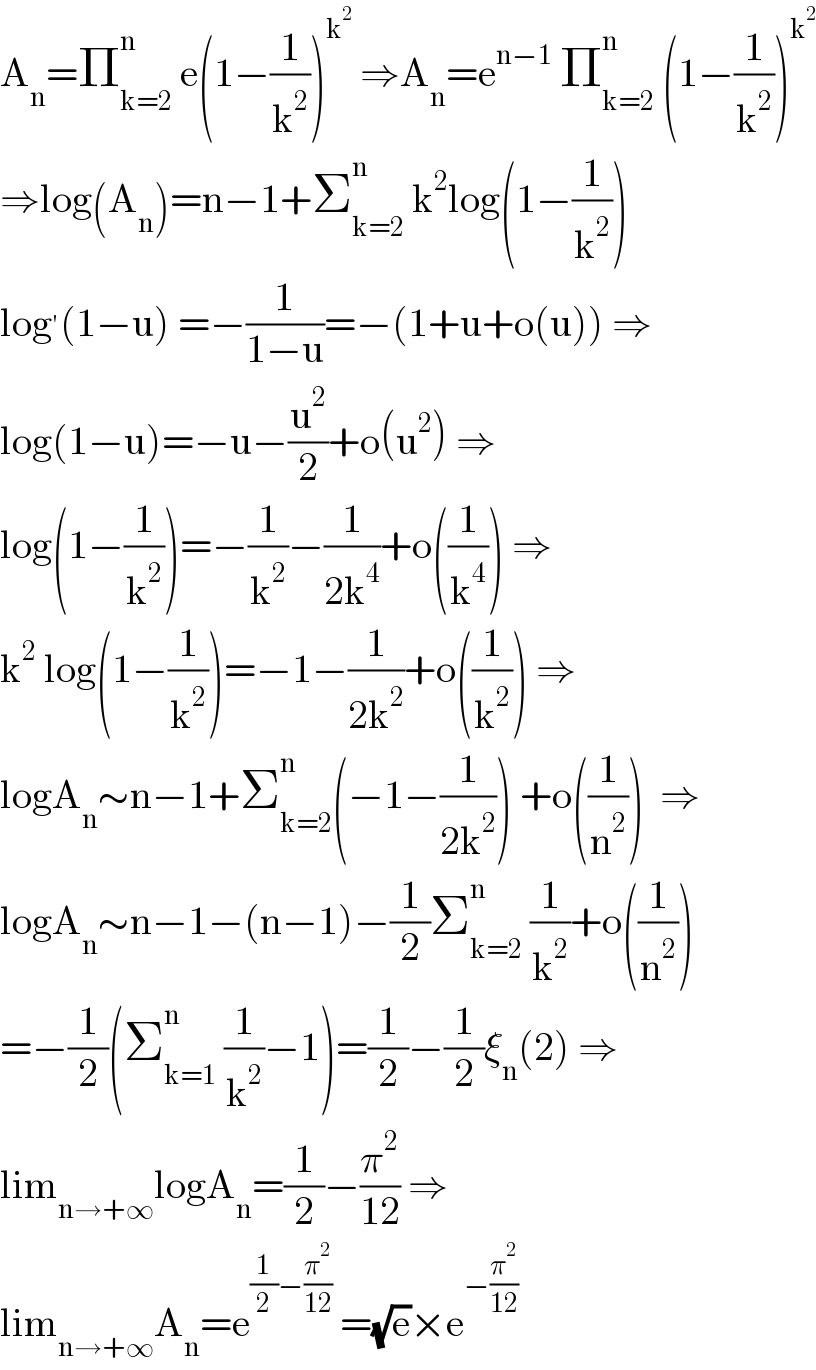
A_n =Π_(k=2) ^n e(1−(1/k^2 ))^k^2 ⇒A_n =e^(n−1) Π_(k=2) ^n (1−(1/k^2 ))^k^2 ⇒log(A_n )=n−1+Σ_(k=2) ^n k^2 log(1−(1/k^2 )) log^′ (1−u) =−(1/(1−u))=−(1+u+o(u)) ⇒ log(1−u)=−u−(u^2 /2)+o(u^2 ) ⇒ log(1−(1/k^2 ))=−(1/k^2 )−(1/(2k^4 ))+o((1/k^4 )) ⇒ k^2 log(1−(1/k^2 ))=−1−(1/(2k^2 ))+o((1/k^2 )) ⇒ logA_n ∼n−1+Σ_(k=2) ^n (−1−(1/(2k^2 ))) +o((1/n^2 )) ⇒ logA_n ∼n−1−(n−1)−(1/2)Σ_(k=2) ^n (1/k^2 )+o((1/n^2 )) =−(1/2)(Σ_(k=1) ^n (1/k^2 )−1)=(1/2)−(1/2)ξ_n (2) ⇒ lim_(n→+∞) logA_n =(1/2)−(π^2 /(12)) ⇒ lim_(n→+∞) A_n =e^((1/2)−(π^2 /(12))) =(√e)×e^(−(π^2 /(12)))

$$\mathrm{A}_{\mathrm{n}} =\prod_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\mathrm{e}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\right)^{\mathrm{k}^{\mathrm{2}} } \:\Rightarrow\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\mathrm{n}−\mathrm{1}} \:\prod_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\right)^{\mathrm{k}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{log}\left(\mathrm{A}_{\mathrm{n}} \right)=\mathrm{n}−\mathrm{1}+\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \mathrm{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\right) \\ $$$$\mathrm{log}^{'} \left(\mathrm{1}−\mathrm{u}\right)\:=−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}}=−\left(\mathrm{1}+\mathrm{u}+\mathrm{o}\left(\mathrm{u}\right)\right)\:\Rightarrow \\ $$$$\mathrm{log}\left(\mathrm{1}−\mathrm{u}\right)=−\mathrm{u}−\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\mathrm{u}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\mathrm{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\right)=−\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{4}} }+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{4}} }\right)\:\Rightarrow \\ $$$$\mathrm{k}^{\mathrm{2}} \:\mathrm{log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\right)=−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$$\mathrm{logA}_{\mathrm{n}} \sim\mathrm{n}−\mathrm{1}+\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \left(−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2k}^{\mathrm{2}} }\right)\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\:\:\Rightarrow \\ $$$$\mathrm{logA}_{\mathrm{n}} \sim\mathrm{n}−\mathrm{1}−\left(\mathrm{n}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{2}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)\: \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\xi_{\mathrm{n}} \left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{logA}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}} \:=\sqrt{\mathrm{e}}×\mathrm{e}^{−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com