Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 148816 by ArielVyny last updated on 31/Jul/21

∫_0 ^∞ x^m e^(ix^n ) dx=??

$$\int_{\mathrm{0}} ^{\infty} {x}^{{m}} {e}^{{ix}^{{n}} } {dx}=?? \\ $$

Answered by mathmax by abdo last updated on 01/Aug/21

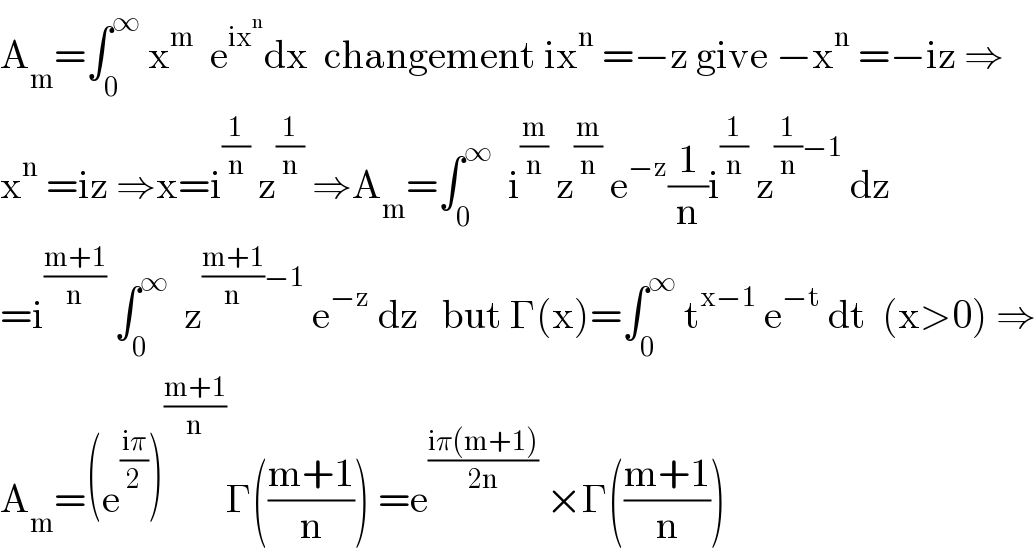
A_m =∫_0 ^∞ x^m e^(ix^n ) dx changement ix^n =−z give −x^n =−iz ⇒ x^n =iz ⇒x=i^(1/n) z^(1/n) ⇒A_m =∫_0 ^∞ i^(m/n) z^(m/n) e^(−z) (1/n)i^(1/n) z^((1/n)−1) dz =i^((m+1)/n) ∫_0 ^∞ z^(((m+1)/n)−1) e^(−z) dz but Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt (x>0) ⇒ A_m =(e^((iπ)/2) )^((m+1)/n) Γ(((m+1)/n)) =e^((iπ(m+1))/(2n)) ×Γ(((m+1)/n))

$$\mathrm{A}_{\mathrm{m}} =\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{m}} \:\:\mathrm{e}^{\mathrm{ix}^{\mathrm{n}} } \mathrm{dx}\:\:\mathrm{changement}\:\mathrm{ix}^{\mathrm{n}} \:=−\mathrm{z}\:\mathrm{give}\:−\mathrm{x}^{\mathrm{n}} \:=−\mathrm{iz}\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{n}} \:=\mathrm{iz}\:\Rightarrow\mathrm{x}=\mathrm{i}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\mathrm{A}_{\mathrm{m}} =\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{i}^{\frac{\mathrm{m}}{\mathrm{n}}} \:\mathrm{z}^{\frac{\mathrm{m}}{\mathrm{n}}} \:\mathrm{e}^{−\mathrm{z}} \frac{\mathrm{1}}{\mathrm{n}}\mathrm{i}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{dz} \\ $$$$=\mathrm{i}^{\frac{\mathrm{m}+\mathrm{1}}{\mathrm{n}}} \:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{z}^{\frac{\mathrm{m}+\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{z}} \:\mathrm{dz}\:\:\:\mathrm{but}\:\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\:\left(\mathrm{x}>\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{m}} =\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{m}+\mathrm{1}}{\mathrm{n}}} \Gamma\left(\frac{\mathrm{m}+\mathrm{1}}{\mathrm{n}}\right)\:=\mathrm{e}^{\frac{\mathrm{i}\pi\left(\mathrm{m}+\mathrm{1}\right)}{\mathrm{2n}}} \:×\Gamma\left(\frac{\mathrm{m}+\mathrm{1}}{\mathrm{n}}\right) \\ $$

Commented by ArielVyny last updated on 01/Aug/21

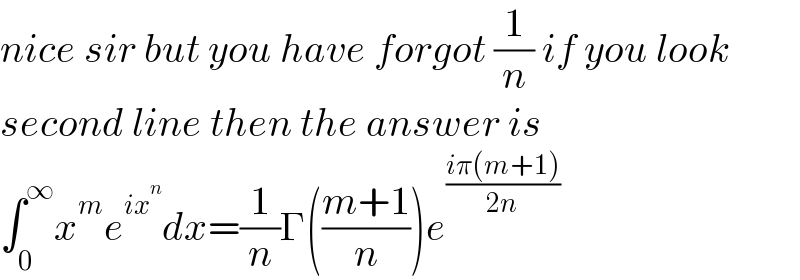
nice sir but you have forgot (1/n) if you look second line then the answer is ∫_0 ^∞ x^m e^(ix^n ) dx=(1/n)Γ(((m+1)/n))e^((iπ(m+1))/(2n))

$${nice}\:{sir}\:{but}\:{you}\:{have}\:{forgot}\:\frac{\mathrm{1}}{{n}}\:{if}\:{you}\:{look} \\ $$$${second}\:{line}\:{then}\:{the}\:{answer}\:{is} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{{m}} {e}^{{ix}^{{n}} } {dx}=\frac{\mathrm{1}}{{n}}\Gamma\left(\frac{{m}+\mathrm{1}}{{n}}\right){e}^{\frac{{i}\pi\left({m}+\mathrm{1}\right)}{\mathrm{2}{n}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com