Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 148825 by DELETED last updated on 31/Jul/21

Answered by DELETED last updated on 31/Jul/21

ΣIR+ΣE=0 i_1 +i_2 =i_3 →i_2 =i_3 −i_2 ......(1) 2i_1 +3i_3 +9−6=0 2i_1 +3i_3 =−3 ....(2) 6i_2 +3i_3 +9−12=0 6i_2 +3i_3 =3 6(i_3 −i_1 )+3i_3 =3 −6i_1 +9i_3 = 3 ....(3) (2)→(3) 2i_1 +3i_3 =−3 ×3 −6i_1 +9i_3 = 3 −−−−−−−+ 6i_1 +9i_3 =−9 −6i_1 +9i_3 = 3 −−−−−−−+ 18i_3 = −6 i_3 = −(1/3) A 2i_1 +3i_3 =−3 2i_1 −1=−3 2i_1 =−2 →i_1 =−1 A i_2 =−(1/3)+1=(2/3) A

$$\Sigma\mathrm{IR}+\Sigma\mathrm{E}=\mathrm{0} \\ $$$$\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{i}_{\mathrm{3}} \:\rightarrow\mathrm{i}_{\mathrm{2}} \:=\mathrm{i}_{\mathrm{3}} −\mathrm{i}_{\mathrm{2}} \:......\left(\mathrm{1}\right) \\ $$$$\mathrm{2i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{3}} +\mathrm{9}−\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{2i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{3}} =−\mathrm{3}\:....\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{6i}_{\mathrm{2}} +\mathrm{3i}_{\mathrm{3}} +\mathrm{9}−\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{6i}_{\mathrm{2}} +\mathrm{3i}_{\mathrm{3}} =\mathrm{3}\: \\ $$$$\mathrm{6}\left(\mathrm{i}_{\mathrm{3}} −\mathrm{i}_{\mathrm{1}} \right)+\mathrm{3i}_{\mathrm{3}} =\mathrm{3} \\ $$$$−\mathrm{6i}_{\mathrm{1}} +\mathrm{9i}_{\mathrm{3}} \:=\:\mathrm{3}\:....\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\rightarrow\left(\mathrm{3}\right)\:\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{3}} =−\mathrm{3}\:\:\:\:×\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6i}_{\mathrm{1}} +\mathrm{9i}_{\mathrm{3}} \:=\:\:\:\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6i}_{\mathrm{1}} +\mathrm{9i}_{\mathrm{3}} =−\mathrm{9}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6i}_{\mathrm{1}} +\mathrm{9i}_{\mathrm{3}} \:=\:\:\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{18i}_{\mathrm{3}} \:=\:−\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{i}_{\mathrm{3}} \:=\:−\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{A} \\ $$$$\:\:\:\:\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{3}} =−\mathrm{3} \\ $$$$\:\:\:\:\:\:\mathrm{2i}_{\mathrm{1}} −\mathrm{1}=−\mathrm{3} \\ $$$$\:\:\:\:\:\:\mathrm{2i}_{\mathrm{1}} =−\mathrm{2}\:\rightarrow\mathrm{i}_{\mathrm{1}} =−\mathrm{1}\:\mathrm{A} \\ $$$$\:\:\:\:\:\:\mathrm{i}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}=\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by JDamian last updated on 31/Jul/21

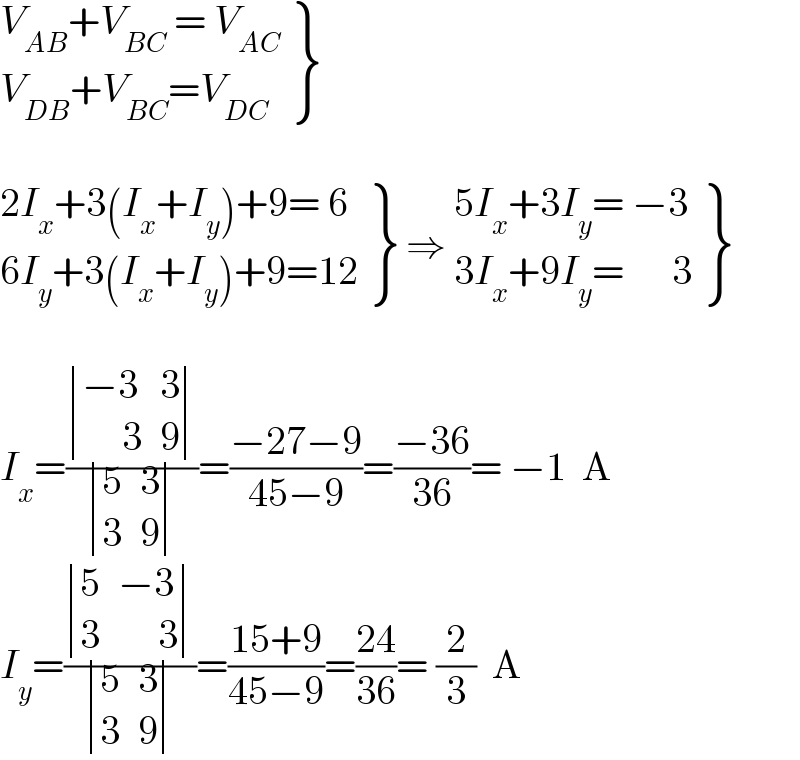
{: ((V_(AB) +V_(BC) = V_(AC) )),((V_(DB) +V_(BC) =V_(DC) )) } {: ((2I_x +3(I_x +I_y )+9= 6)),((6I_y +3(I_x +I_y )+9=12)) } ⇒ {: ((5I_x +3I_y = −3)),((3I_x +9I_y = 3)) } I_x =( determinant (((−3),3),(( 3),9))/ determinant ((5,3),(3,9)))=((−27−9)/(45−9))=((−36)/(36))= −1 A I_y =( determinant ((5,(−3)),(3,( 3)))/ determinant ((5,3),(3,9)))=((15+9)/(45−9))=((24)/(36))= (2/3) A

$$\left.\begin{matrix}{{V}_{{AB}} +{V}_{{BC}} \:=\:{V}_{{AC}} }\\{{V}_{{DB}} +{V}_{{BC}} ={V}_{{DC}} }\end{matrix}\right\} \\ $$$$ \\ $$$$\left.\begin{matrix}{\mathrm{2}{I}_{{x}} +\mathrm{3}\left({I}_{{x}} +{I}_{{y}} \right)+\mathrm{9}=\:\mathrm{6}}\\{\mathrm{6}{I}_{{y}} +\mathrm{3}\left({I}_{{x}} +{I}_{{y}} \right)+\mathrm{9}=\mathrm{12}}\end{matrix}\right\}\:\Rightarrow\:\left.\begin{matrix}{\mathrm{5}{I}_{{x}} +\mathrm{3}{I}_{{y}} =\:−\mathrm{3}}\\{\mathrm{3}{I}_{{x}} +\mathrm{9}{I}_{{y}} =\:\:\:\:\:\:\mathrm{3}}\end{matrix}\right\} \\ $$$$ \\ $$$${I}_{{x}} =\frac{\begin{vmatrix}{−\mathrm{3}}&{\mathrm{3}}\\{\:\:\:\:\:\mathrm{3}}&{\mathrm{9}}\end{vmatrix}}{\begin{vmatrix}{\mathrm{5}}&{\mathrm{3}}\\{\mathrm{3}}&{\mathrm{9}}\end{vmatrix}}=\frac{−\mathrm{27}−\mathrm{9}}{\mathrm{45}−\mathrm{9}}=\frac{−\mathrm{36}}{\mathrm{36}}=\:−\mathrm{1}\:\:\mathrm{A} \\ $$$${I}_{{y}} =\frac{\begin{vmatrix}{\mathrm{5}}&{−\mathrm{3}}\\{\mathrm{3}}&{\:\:\:\:\:\mathrm{3}}\end{vmatrix}}{\begin{vmatrix}{\mathrm{5}}&{\mathrm{3}}\\{\mathrm{3}}&{\mathrm{9}}\end{vmatrix}}=\frac{\mathrm{15}+\mathrm{9}}{\mathrm{45}−\mathrm{9}}=\frac{\mathrm{24}}{\mathrm{36}}=\:\frac{\mathrm{2}}{\mathrm{3}}\:\:\mathrm{A} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com