
Question Number 148887 by mathdanisur last updated on 01/Aug/21
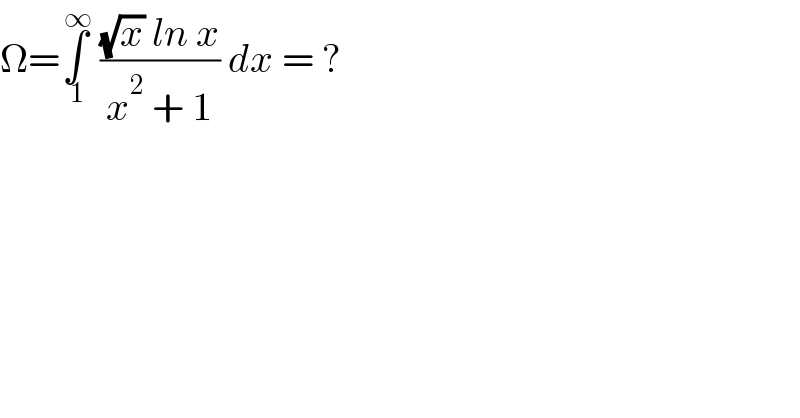
$$\Omega=\underset{\:\mathrm{1}} {\overset{\:\infty} {\int}}\:\frac{\sqrt{{x}}\:{ln}\:{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:=\:? \\ $$
Answered by Kamel last updated on 01/Aug/21
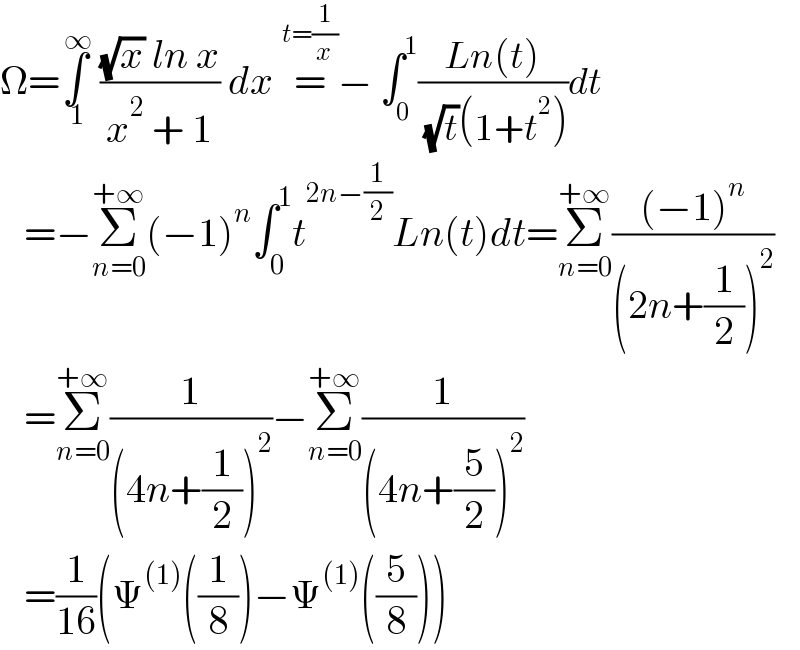
$$\Omega=\underset{\:\mathrm{1}} {\overset{\:\infty} {\int}}\:\frac{\sqrt{{x}}\:{ln}\:{x}}{{x}^{\mathrm{2}} \:+\:\mathrm{1}}\:{dx}\:\overset{{t}=\frac{\mathrm{1}}{{x}}} {=}−\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left({t}\right)}{\:\sqrt{{t}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$\:\:\:=−\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{n}−\frac{\mathrm{1}}{\mathrm{2}}} {Ln}\left({t}\right){dt}=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4}{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }−\underset{{n}=\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4}{n}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{16}}\left(\Psi^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{1}}{\mathrm{8}}\right)−\Psi^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{5}}{\mathrm{8}}\right)\right) \\ $$
Commented by mathdanisur last updated on 01/Aug/21

$${Thank}\:{you}\:{Ser} \\ $$
Answered by Ank0369 last updated on 01/Aug/21
![Solution: Ω =^(x=1/y) ∫_0 ^( 1) −((log_e (y))/( (√y)(1+y^2 ))) dy =^(y=x^2 ) ∫_0 ^( 1) −4((log_e (x))/(1+x^4 ))dx −(Ω/4) = Σ_(n=0) ^(n=∞) (−1)^n ∫_0 ^( 1) x^(4n) ∙log_e (x)dx ⇒ Σ_(n=0) ^(n=∞) (((−1)^(n+1) )/((4n+1)^2 )) −4Ω = Σ_(n=0) ^(n=∞) (((−1)^(n+1) )/((n+(1/4))^2 )) ⇒ (1/4)[ζ(2,(5/8))−ζ(2,(1/8))] Ω = ∫_1 ^∞ (((√x)∙log_e (x))/(x^2 +1))dx = (1/(16))[ψ^((1)) ((1/8))−ψ^((1)) ((5/8))]](Q148898.png)
$${Solution}:\:\Omega\:\overset{{x}=\mathrm{1}/{y}} {=}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} −\frac{\mathrm{log}_{{e}} \left({y}\right)}{\:\sqrt{{y}}\left(\mathrm{1}+{y}^{\mathrm{2}} \right)}\:{dy}\:\:\overset{{y}={x}^{\mathrm{2}} } {=}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} −\mathrm{4}\frac{\mathrm{log}_{{e}} \left({x}\right)}{\mathrm{1}+{x}^{\mathrm{4}} }{dx}\: \\ $$$$−\frac{\Omega}{\mathrm{4}}\:=\:\underset{{n}=\mathrm{0}} {\overset{{n}=\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\mathrm{4}{n}} \centerdot\mathrm{log}_{{e}} \left({x}\right){dx}\:\Rightarrow\:\underset{{n}=\mathrm{0}} {\overset{{n}=\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{4}{n}+\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$−\mathrm{4}\Omega\:=\:\underset{{n}=\mathrm{0}} {\overset{{n}=\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{4}}\left[\zeta\left(\mathrm{2},\frac{\mathrm{5}}{\mathrm{8}}\right)−\zeta\left(\mathrm{2},\frac{\mathrm{1}}{\mathrm{8}}\right)\right] \\ $$$$\Omega\:=\:\int_{\mathrm{1}} ^{\infty} \frac{\sqrt{{x}}\centerdot\mathrm{log}_{{e}} \left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:=\:\frac{\mathrm{1}}{\mathrm{16}}\left[\psi^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{1}}{\mathrm{8}}\right)−\psi^{\left(\mathrm{1}\right)} \left(\frac{\mathrm{5}}{\mathrm{8}}\right)\right]\: \\ $$$$\: \\ $$
