Question Number 149024 by mathdanisur last updated on 02/Aug/21

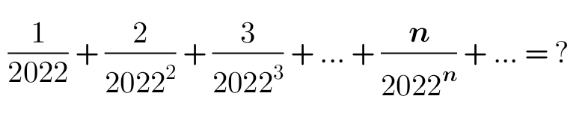
Answered by Olaf_Thorendsen last updated on 02/Aug/21

f_n (x) = Σ_(k=1) ^n x^k = x((1−x^n )/(1−x)) = ((x−x^(n+1) )/(1−x)) x.f′(x) = xΣ_(k=1) ^n kx^(k−1) = Σ_(k=1) ^n kx^k x.f′(x) = x[(((1−(n+1)x^n )(1−x)+(x−x^(n+1) ))/((1−x)^2 ))] x.f′(x) = ((x−(n+1)x^(n+1) +nx^(n+2) )/((1−x)^2 )) For x = (1/(2022)) : Σ_(k=1) ^n (k/(2022^k )) = (((1/(2022))−((n+1)/(2022^(n+1) ))+(n/(2022^(n+2) )))/((((2021)/(2022)))^2 )) Σ_(k=1) ^n (k/(2022^k )) = ((2022)/(2021^2 )).(1−((n+1)/(2022^n ))+(n/(2022^(n+1) )))

Commented bymathdanisur last updated on 02/Aug/21

Thank You Ser Answer: ((2022)/(2021^2 ))

Answered by prakash jain last updated on 02/Aug/21

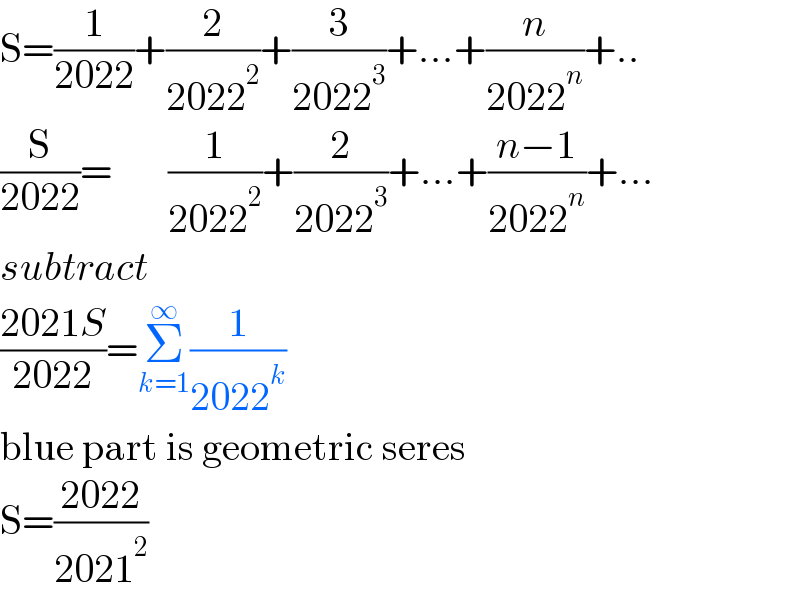
S=(1/(2022))+(2/(2022^2 ))+(3/(2022^3 ))+...+(n/(2022^n ))+.. (S/(2022))= (1/(2022^2 ))+(2/(2022^3 ))+...+((n−1)/(2022^n ))+... subtract ((2021S)/(2022))=Σ_(k=1) ^∞ (1/(2022^k )) blue part is geometric seres S=((2022)/(2021^2 ))

Commented bymathdanisur last updated on 02/Aug/21

Thank You Ser

Commented byOlaf_Thorendsen last updated on 02/Aug/21

Excellent !