Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 149031 by puissant last updated on 02/Aug/21

Answered by EDWIN88 last updated on 02/Aug/21

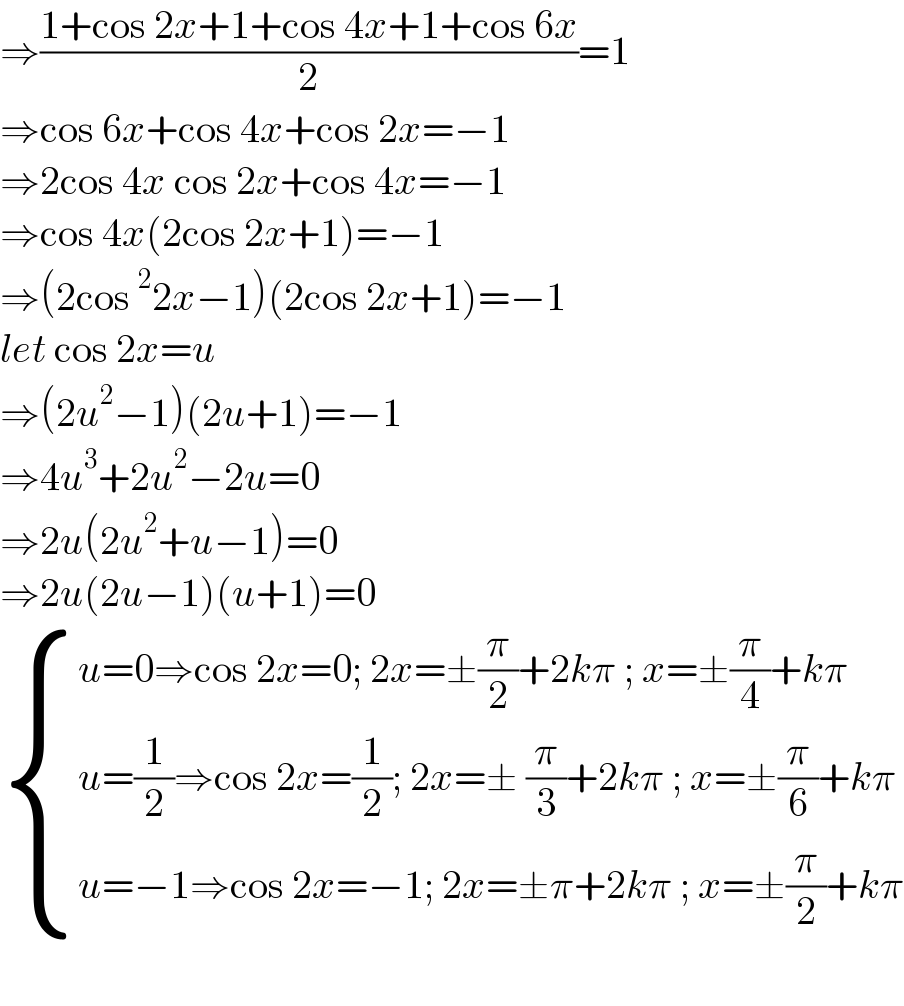
⇒((1+cos 2x+1+cos 4x+1+cos 6x)/2)=1 ⇒cos 6x+cos 4x+cos 2x=−1 ⇒2cos 4x cos 2x+cos 4x=−1 ⇒cos 4x(2cos 2x+1)=−1 ⇒(2cos^2 2x−1)(2cos 2x+1)=−1 let cos 2x=u ⇒(2u^2 −1)(2u+1)=−1 ⇒4u^3 +2u^2 −2u=0 ⇒2u(2u^2 +u−1)=0 ⇒2u(2u−1)(u+1)=0 { ((u=0⇒cos 2x=0; 2x=±(π/2)+2kπ ; x=±(π/4)+kπ)),((u=(1/2)⇒cos 2x=(1/2); 2x=± (π/3)+2kπ ; x=±(π/6)+kπ )),((u=−1⇒cos 2x=−1; 2x=±π+2kπ ; x=±(π/2)+kπ)) :}

$$\Rightarrow\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}+\mathrm{1}+\mathrm{cos}\:\mathrm{4}{x}+\mathrm{1}+\mathrm{cos}\:\mathrm{6}{x}}{\mathrm{2}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{6}{x}+\mathrm{cos}\:\mathrm{4}{x}+\mathrm{cos}\:\mathrm{2}{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{2}{x}+\mathrm{cos}\:\mathrm{4}{x}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{4}{x}\left(\mathrm{2cos}\:\mathrm{2}{x}+\mathrm{1}\right)=−\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{2cos}\:\mathrm{2}{x}+\mathrm{1}\right)=−\mathrm{1} \\ $$$${let}\:\mathrm{cos}\:\mathrm{2}{x}={u} \\ $$$$\Rightarrow\left(\mathrm{2}{u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{u}+\mathrm{1}\right)=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{4}{u}^{\mathrm{3}} +\mathrm{2}{u}^{\mathrm{2}} −\mathrm{2}{u}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{u}\left(\mathrm{2}{u}^{\mathrm{2}} +{u}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{u}\left(\mathrm{2}{u}−\mathrm{1}\right)\left({u}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\begin{cases}{{u}=\mathrm{0}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}=\mathrm{0};\:\mathrm{2}{x}=\pm\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\:;\:{x}=\pm\frac{\pi}{\mathrm{4}}+{k}\pi}\\{{u}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}=\frac{\mathrm{1}}{\mathrm{2}};\:\mathrm{2}{x}=\pm\:\frac{\pi}{\mathrm{3}}+\mathrm{2}{k}\pi\:;\:{x}=\pm\frac{\pi}{\mathrm{6}}+{k}\pi\:}\\{{u}=−\mathrm{1}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}=−\mathrm{1};\:\mathrm{2}{x}=\pm\pi+\mathrm{2}{k}\pi\:;\:{x}=\pm\frac{\pi}{\mathrm{2}}+{k}\pi}\end{cases} \\ $$$$ \\ $$

Commented by puissant last updated on 02/Aug/21

thanks...

$$\mathrm{thanks}... \\ $$

Answered by MJS_new last updated on 02/Aug/21

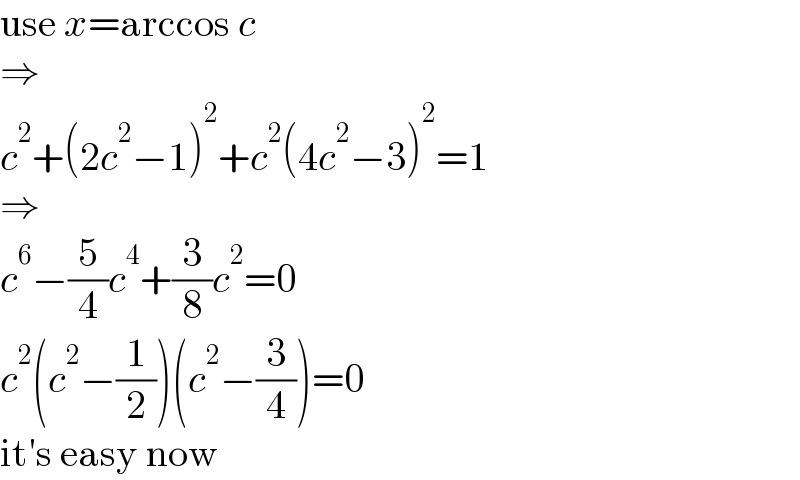
use x=arccos c ⇒ c^2 +(2c^2 −1)^2 +c^2 (4c^2 −3)^2 =1 ⇒ c^6 −(5/4)c^4 +(3/8)c^2 =0 c^2 (c^2 −(1/2))(c^2 −(3/4))=0 it′s easy now

$$\mathrm{use}\:{x}=\mathrm{arccos}\:{c} \\ $$$$\Rightarrow \\ $$$${c}^{\mathrm{2}} +\left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} \left(\mathrm{4}{c}^{\mathrm{2}} −\mathrm{3}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow \\ $$$${c}^{\mathrm{6}} −\frac{\mathrm{5}}{\mathrm{4}}{c}^{\mathrm{4}} +\frac{\mathrm{3}}{\mathrm{8}}{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${c}^{\mathrm{2}} \left({c}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\right)\left({c}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{now} \\ $$

Commented by puissant last updated on 02/Aug/21

thanks..

$$\mathrm{thanks}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com