
Question Number 14905 by ajfour last updated on 05/Jun/17
Commented by ajfour last updated on 05/Jun/17
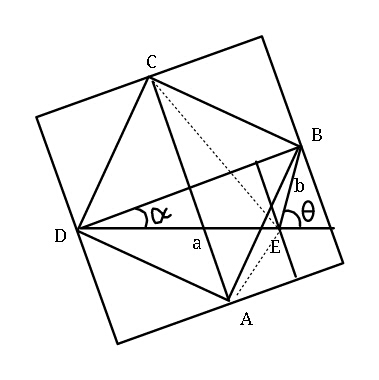
![Q. 14797 (construction method) given DE=a, EB=b ; find Area of △AEC. let diagonal of square=2s 2s=acos α+bcos (θ−α) s=(1/2)(acos α+bcos (θ−α)) ...(i) let ⊥ distance of E from AC be h. h=s−bcos (θ−α) h=(1/2)(acos α−bcos (θ−α)) ...(ii) tan α=((sin α)/(cos α))=((bsin θ)/(a+bcos θ)) ⇒ asin α=b(sin θcos α−cos θsin α) or asin α = bsin (θ−α) ...(iii) Area of △AEC =(1/2)(2s)h=sh =(1/4)[a^2 cos^2 α−b^2 cos^2 (θ−α)] [using (i) and (ii)] =(1/4)[a^2 −a^2 sin^2 α−b^2 +b^2 sin^2 (θ−α)] Area_(△AEC) =(1/4)(a^2 −b^2 ) . [using (iii)] .](Q14907.png)
$${Q}.\:\mathrm{14797}\:\left({construction}\:{method}\right) \\ $$$${given}\:{DE}={a},\:\:{EB}={b}\:;\:{find} \\ $$$${Area}\:{of}\:\bigtriangleup{AEC}. \\ $$$$ \\ $$$${let}\:{diagonal}\:{of}\:{square}=\mathrm{2}{s} \\ $$$$\mathrm{2}{s}={a}\mathrm{cos}\:\alpha+{b}\mathrm{cos}\:\left(\theta−\alpha\right) \\ $$$$\:{s}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}\mathrm{cos}\:\alpha+{b}\mathrm{cos}\:\left(\theta−\alpha\right)\right)\:\:...\left({i}\right) \\ $$$${let}\:\bot\:{distance}\:{of}\:{E}\:{from}\:{AC}\:{be}\:{h}. \\ $$$$\:\:{h}={s}−{b}\mathrm{cos}\:\left(\theta−\alpha\right) \\ $$$$\:\:{h}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}\mathrm{cos}\:\alpha−{b}\mathrm{cos}\:\left(\theta−\alpha\right)\right)\:\:...\left({ii}\right) \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}=\frac{{b}\mathrm{sin}\:\theta}{{a}+{b}\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\:\:{a}\mathrm{sin}\:\alpha={b}\left(\mathrm{sin}\:\theta\mathrm{cos}\:\alpha−\mathrm{cos}\:\theta\mathrm{sin}\:\alpha\right) \\ $$$${or}\:\:\:{a}\mathrm{sin}\:\alpha\:=\:{b}\mathrm{sin}\:\left(\theta−\alpha\right)\:\:\:\:\:\:...\left({iii}\right) \\ $$$${Area}\:{of}\:\bigtriangleup{AEC}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{s}\right){h}={sh} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{4}}\left[{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha−{b}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \left(\theta−\alpha\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{using}\:\left({i}\right)\:{and}\:\left({ii}\right)\right] \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{4}}\left[{a}^{\mathrm{2}} −{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \alpha−{b}^{\mathrm{2}} +{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \left(\theta−\alpha\right)\right] \\ $$$$\:{Area}_{\bigtriangleup{AEC}} \:=\frac{\mathrm{1}}{\mathrm{4}}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\:. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{using}\:\left({iii}\right)\right]\:. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17
$${god}\:{bless}\:{you}\:{mr}\:{Ajfour}.{it}\:{is}\:{a}\:{beautiful} \\ $$$${prove}.{i}\:{love}\:{it}\:{very}\:{much}.{thanks}. \\ $$
Commented by ajfour last updated on 05/Jun/17

$${thanks}\:{sir},\:{i}\:{was}\:{curious}\:{about} \\ $$$${the}\:{independence}\:{of}\:{the}\:{concerned} \\ $$$${area}\:{with}\:\theta\:.{It}\:{is}\:{still}\:{not}\:{clear}\:{to} \\ $$$${me}..! \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 05/Jun/17
$${for}\:{what}?\:{the}\:{area}\:{computed}\:{finally} \\ $$$${whit}\:{no}\:{independence}\:{to}\:\theta. \\ $$
Commented by ajfour last updated on 05/Jun/17
$${i}\:{mean}\:{i}\:{it}\:{is}\:{lengthy},\:{not}\:{direct} \\ $$$${or}\:{obvious}\:{as}\:{it}\:{is}\:{to}\:{mrW}\mathrm{1}.. \\ $$
