
Question Number 149273 by john_santu last updated on 04/Aug/21
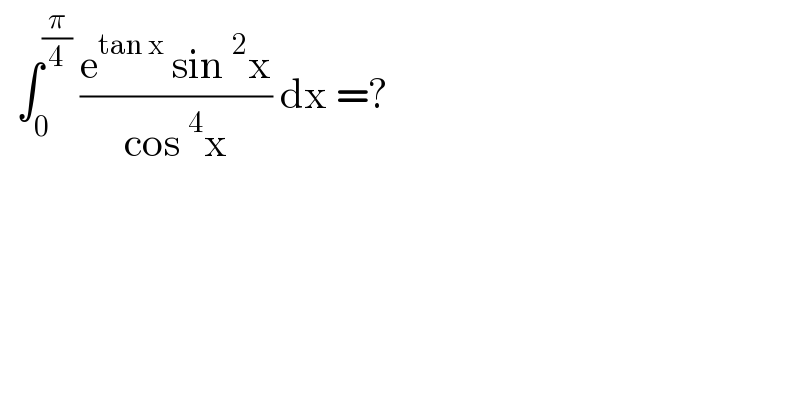
$$\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{e}^{\mathrm{tan}\:\mathrm{x}} \:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}\:\mathrm{dx}\:=? \\ $$
Answered by Ar Brandon last updated on 04/Aug/21
![I=∫_0 ^(π/4) ((e^(tanx) sin^2 x)/(cos^4 x))dx=∫_0 ^(π/4) e^(tanx) sec^2 x∙tan^2 xdx =[e^(tanx) ∙tan^2 x]_0 ^(π/4) −2∫_0 ^(π/4) e^(tanx) sec^2 x∙tanxdx =e−2[e^(tanx) tanx]_0 ^(π/4) +2∫_0 ^(π/4) e^(tanx) sec^2 xdx =e−2e+2[e^(tanx) ]_0 ^(π/4) =−e+2(e−1)=e−2](Q149282.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{e}^{\mathrm{tan}{x}} \mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{cos}^{\mathrm{4}} {x}}{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {e}^{\mathrm{tan}{x}} \mathrm{sec}^{\mathrm{2}} {x}\centerdot\mathrm{tan}^{\mathrm{2}} {xdx} \\ $$$$\:\:\:=\left[{e}^{\mathrm{tan}{x}} \centerdot\mathrm{tan}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {e}^{\mathrm{tan}{x}} \mathrm{sec}^{\mathrm{2}} {x}\centerdot\mathrm{tan}{xdx} \\ $$$$\:\:\:={e}−\mathrm{2}\left[{e}^{\mathrm{tan}{x}} \mathrm{tan}{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} +\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {e}^{\mathrm{tan}{x}} \mathrm{sec}^{\mathrm{2}} {xdx} \\ $$$$\:\:\:={e}−\mathrm{2}{e}+\mathrm{2}\left[{e}^{\mathrm{tan}{x}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =−{e}+\mathrm{2}\left({e}−\mathrm{1}\right)={e}−\mathrm{2} \\ $$
Commented by Ar Brandon last updated on 04/Aug/21
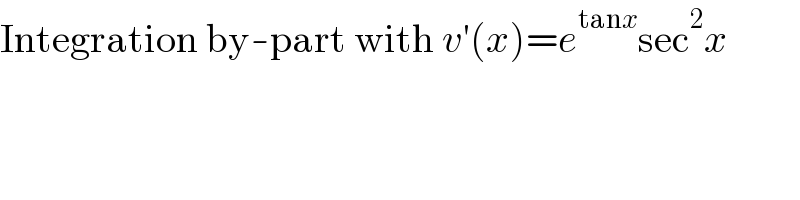
$$\mathrm{Integration}\:\mathrm{by}-\mathrm{part}\:\mathrm{with}\:{v}'\left({x}\right)={e}^{\mathrm{tan}{x}} \mathrm{sec}^{\mathrm{2}} {x} \\ $$
Commented by puissant last updated on 30/Aug/21

$${hummm} \\ $$
Answered by john_santu last updated on 04/Aug/21
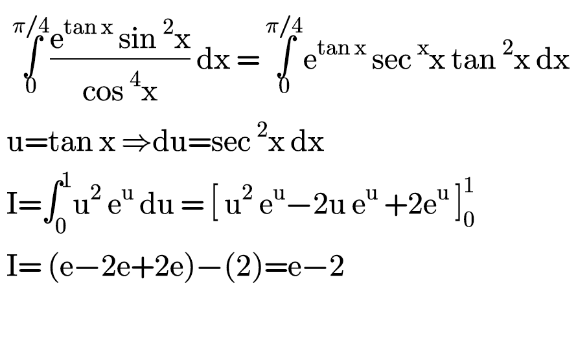
Answered by ArielVyny last updated on 04/Aug/21
![∫_0 ^(π/4) (e^(tanx) /(cos^2 x))×tan^2 xdx t=tanx→dt=(1/(cos^2 x))dx ∫_0 ^1 e^t ×t^2 dt→ { ((du=e^t →u=e^t )),((v=t^2 →dv=2t)) :} ∫_0 ^1 t^2 e^t dt=[t^2 e^t ]_0 ^1 −2∫_0 ^1 e^t t=e^1 −2∫_0 ^1 e^t tdt { ((du=e^t →u=e^t )),((v=t→dv=1)) :} ∫_0 ^1 te^t dt=[te^t ]_0 ^1 −∫_0 ^1 e^t dt=[e^t (t−1)]_0 ^1 =1 ∫_0 ^(π/4) ((e^(tanx) sin^2 x)/(cos^4 x))dx=e^1 −2](Q149306.png)
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{e}^{{tanx}} }{{cos}^{\mathrm{2}} {x}}×{tan}^{\mathrm{2}} {xdx} \\ $$$${t}={tanx}\rightarrow{dt}=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} ×{t}^{\mathrm{2}} {dt}\rightarrow\begin{cases}{{du}={e}^{{t}} \rightarrow{u}={e}^{{t}} }\\{{v}={t}^{\mathrm{2}} \rightarrow{dv}=\mathrm{2}{t}}\end{cases} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} {e}^{{t}} {dt}=\left[{t}^{\mathrm{2}} {e}^{{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} {t}={e}^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} {tdt} \\ $$$$\begin{cases}{{du}={e}^{{t}} \rightarrow{u}={e}^{{t}} }\\{{v}={t}\rightarrow{dv}=\mathrm{1}}\end{cases} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {te}^{{t}} {dt}=\left[{te}^{{t}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} {dt}=\left[{e}^{{t}} \left({t}−\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{e}^{{tanx}} {sin}^{\mathrm{2}} {x}}{{cos}^{\mathrm{4}} {x}}{dx}={e}^{\mathrm{1}} −\mathrm{2} \\ $$
