Question Number 149317 by tabata last updated on 04/Aug/21

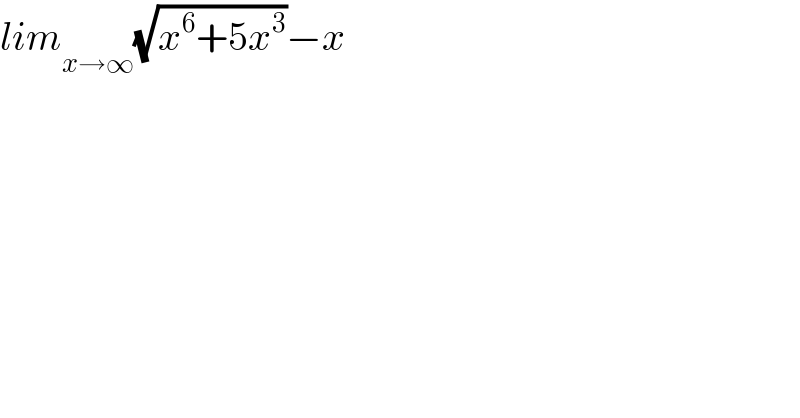
lim_(x→∞) (√(x^6 +5x^3 ))−x

Answered by EDWIN88 last updated on 04/Aug/21

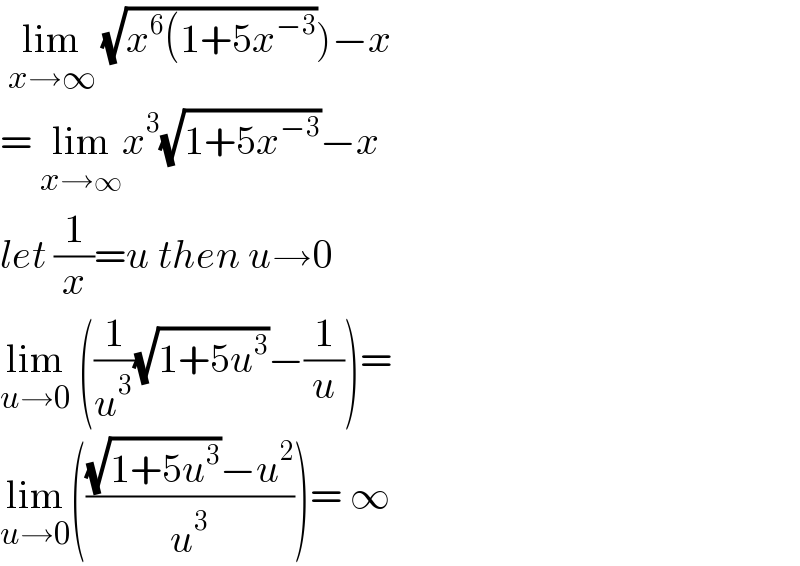
lim_(x→∞) (√(x^6 (1+5x^(−3) )))−x = lim_(x→∞) x^3 (√(1+5x^(−3) ))−x let (1/x)=u then u→0 lim_(u→0) ((1/u^3 )(√(1+5u^3 ))−(1/u))= lim_(u→0) ((((√(1+5u^3 ))−u^2 )/u^3 ))= ∞

Commented byEDWIN88 last updated on 04/Aug/21

yes

Commented byJDamian last updated on 04/Aug/21

in the second line, that 0 is actually an infinity

Answered by mathmax by abdo last updated on 04/Aug/21

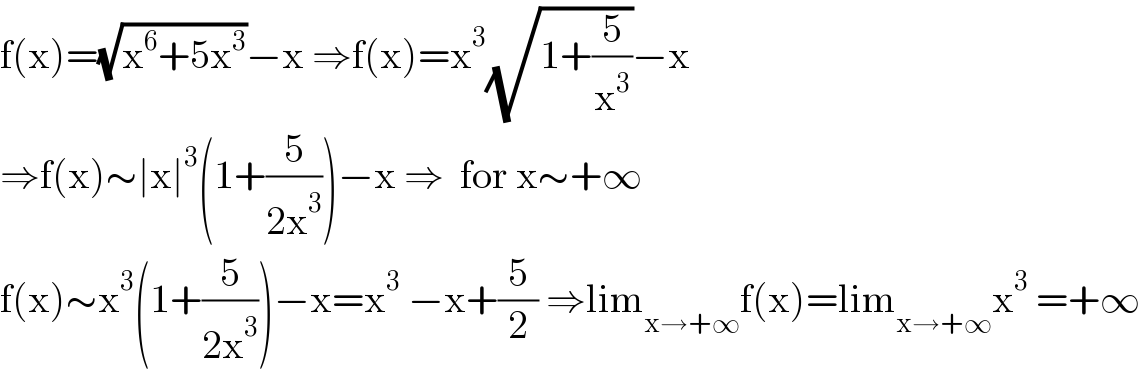
f(x)=(√(x^6 +5x^3 ))−x ⇒f(x)=x^3 (√(1+(5/x^3 )))−x ⇒f(x)∼∣x∣^3 (1+(5/(2x^3 )))−x ⇒ for x∼+∞ f(x)∼x^3 (1+(5/(2x^3 )))−x=x^3 −x+(5/2) ⇒lim_(x→+∞) f(x)=lim_(x→+∞) x^3 =+∞

Commented bymathmax by abdo last updated on 04/Aug/21

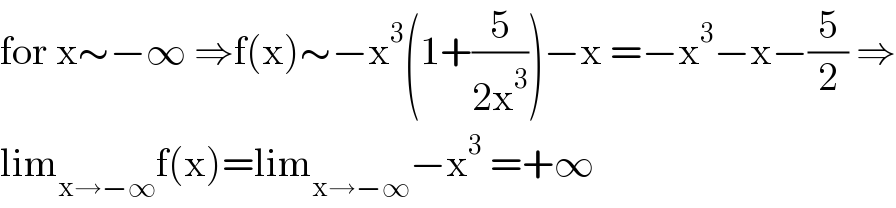
for x∼−∞ ⇒f(x)∼−x^3 (1+(5/(2x^3 )))−x =−x^3 −x−(5/2) ⇒ lim_(x→−∞) f(x)=lim_(x→−∞) −x^3 =+∞