Question Number 149378 by fotosy2k last updated on 05/Aug/21

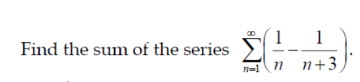
Answered by Ar Brandon last updated on 05/Aug/21

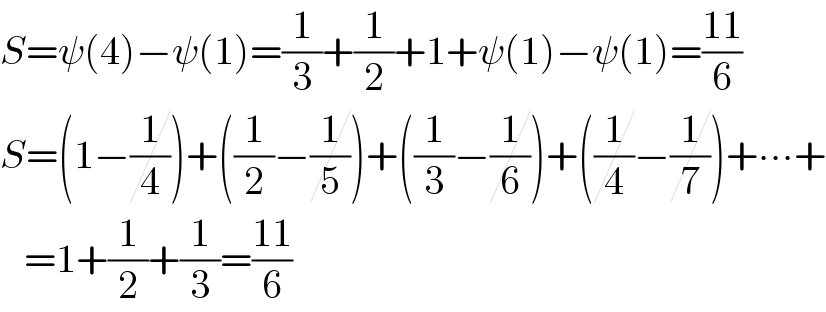
S=ψ(4)−ψ(1)=(1/3)+(1/2)+1+ψ(1)−ψ(1)=((11)/6) S=(1−(1/4))+((1/2)−(1/5))+((1/3)−(1/6))+((1/4)−(1/7))+∙∙∙+ =1+(1/2)+(1/3)=((11)/6)

Answered by gsk2684 last updated on 13/Sep/21

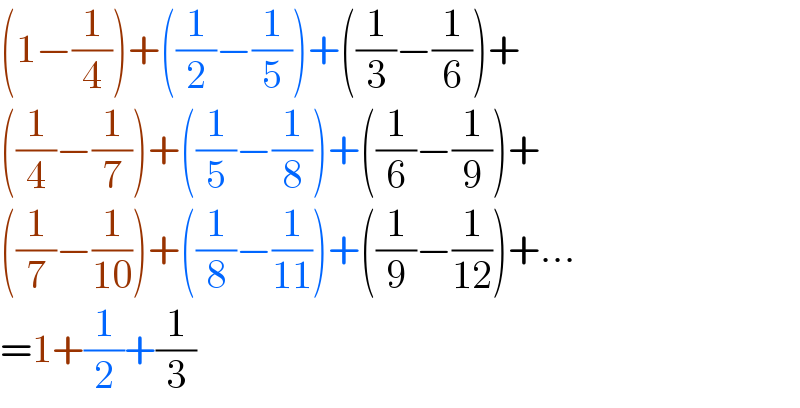
(1−(1/4))+((1/2)−(1/5))+((1/3)−(1/6))+ ((1/4)−(1/7))+((1/5)−(1/8))+((1/6)−(1/9))+ ((1/7)−(1/(10)))+((1/8)−(1/(11)))+((1/9)−(1/(12)))+... =1+(1/2)+(1/3)

Answered by mathmax by abdo last updated on 05/Aug/21

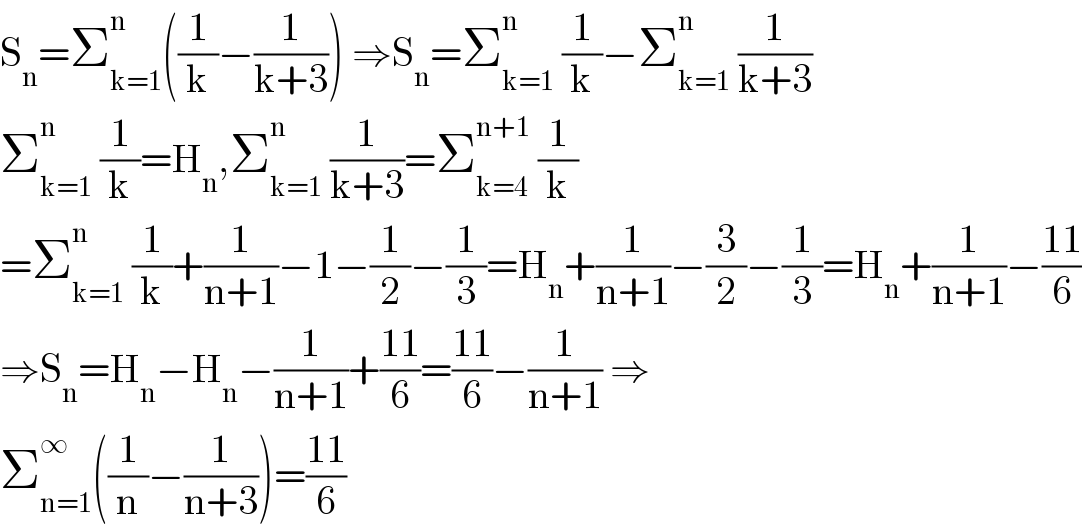
S_n =Σ_(k=1) ^n ((1/k)−(1/(k+3))) ⇒S_n =Σ_(k=1) ^n (1/k)−Σ_(k=1) ^n (1/(k+3)) Σ_(k=1) ^n (1/k)=H_n ,Σ_(k=1) ^n (1/(k+3))=Σ_(k=4) ^(n+1) (1/k) =Σ_(k=1) ^n (1/k)+(1/(n+1))−1−(1/2)−(1/3)=H_n +(1/(n+1))−(3/2)−(1/3)=H_n +(1/(n+1))−((11)/6) ⇒S_n =H_n −H_n −(1/(n+1))+((11)/6)=((11)/6)−(1/(n+1)) ⇒ Σ_(n=1) ^∞ ((1/n)−(1/(n+3)))=((11)/6)

Commented byfotosy2k last updated on 05/Aug/21

thank you