Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 149410 by mathdanisur last updated on 05/Aug/21

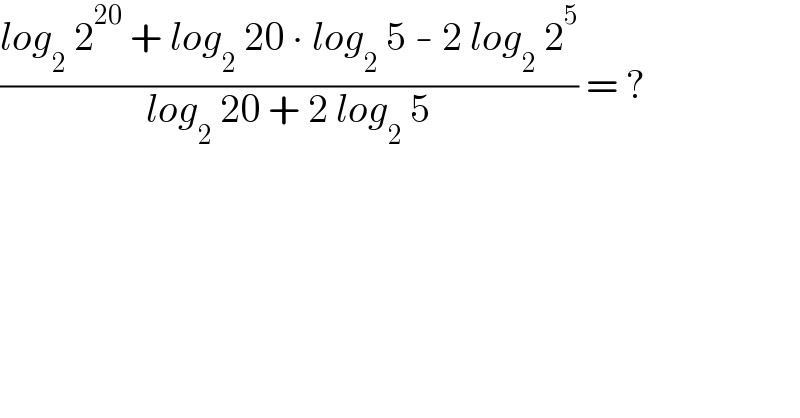
((log_2 2^(20) + log_2 20 ∙ log_2 5 - 2 log_2 2^5 )/(log_2 20 + 2 log_2 5)) = ?

$$\frac{{log}_{\mathrm{2}} \:\mathrm{2}^{\mathrm{20}} \:+\:{log}_{\mathrm{2}} \:\mathrm{20}\:\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:-\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{2}^{\mathrm{5}} }{{log}_{\mathrm{2}} \:\mathrm{20}\:+\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:=\:? \\ $$

Answered by Rasheed.Sindhi last updated on 05/Aug/21

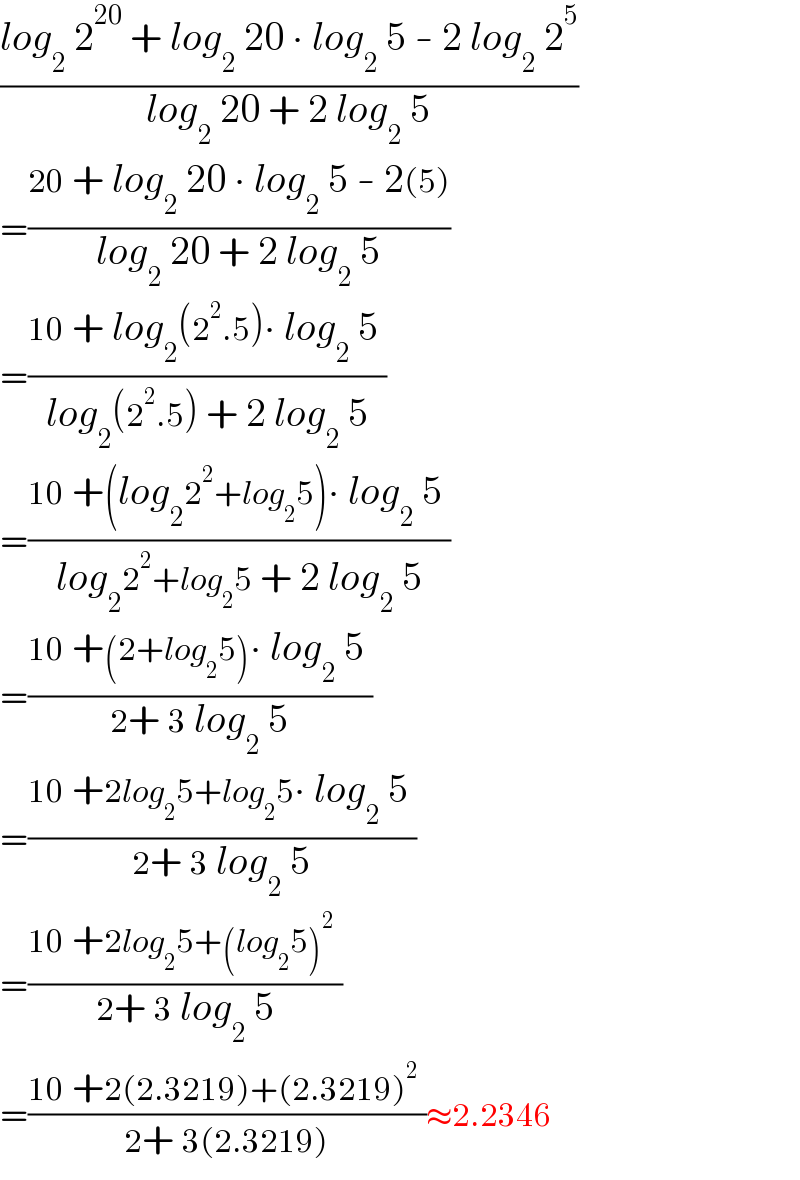
((log_2 2^(20) + log_2 20 ∙ log_2 5 - 2 log_2 2^5 )/(log_2 20 + 2 log_2 5)) =((20 + log_2 20 ∙ log_2 5 - 2(5))/(log_2 20 + 2 log_2 5)) =((10 + log_2 (2^2 .5)∙ log_2 5 )/(log_2 (2^2 .5) + 2 log_2 5)) =((10 +(log_2 2^2 +log_2 5)∙ log_2 5 )/(log_2 2^2 +log_2 5 + 2 log_2 5)) =((10 +(2+log_2 5)∙ log_2 5 )/(2+ 3 log_2 5)) =((10 +2log_2 5+log_2 5∙ log_2 5 )/(2+ 3 log_2 5)) =((10 +2log_2 5+(log_2 5)^2 )/(2+ 3 log_2 5)) =((10 +2(2.3219)+(2.3219)^2 )/(2+ 3(2.3219)))≈2.2346

$$\frac{{log}_{\mathrm{2}} \:\mathrm{2}^{\mathrm{20}} \:+\:{log}_{\mathrm{2}} \:\mathrm{20}\:\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:-\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{2}^{\mathrm{5}} }{{log}_{\mathrm{2}} \:\mathrm{20}\:+\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{5}}\: \\ $$$$=\frac{\mathrm{20}\:+\:{log}_{\mathrm{2}} \:\mathrm{20}\:\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:-\:\mathrm{2}\left(\mathrm{5}\right)}{{log}_{\mathrm{2}} \:\mathrm{20}\:+\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:\: \\ $$$$=\frac{\mathrm{10}\:+\:{log}_{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} .\mathrm{5}\right)\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:}{{log}_{\mathrm{2}} \left(\mathrm{2}^{\mathrm{2}} .\mathrm{5}\right)\:+\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:\: \\ $$$$=\frac{\mathrm{10}\:+\left({log}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}} +{log}_{\mathrm{2}} \mathrm{5}\right)\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:}{{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}} +{log}_{\mathrm{2}} \mathrm{5}\:+\:\mathrm{2}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:\: \\ $$$$=\frac{\mathrm{10}\:+\left(\mathrm{2}+{log}_{\mathrm{2}} \mathrm{5}\right)\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:}{\mathrm{2}+\:\mathrm{3}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:\: \\ $$$$=\frac{\mathrm{10}\:+\mathrm{2}{log}_{\mathrm{2}} \mathrm{5}+{log}_{\mathrm{2}} \mathrm{5}\centerdot\:{log}_{\mathrm{2}} \:\mathrm{5}\:}{\mathrm{2}+\:\mathrm{3}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:\: \\ $$$$=\frac{\mathrm{10}\:+\mathrm{2}{log}_{\mathrm{2}} \mathrm{5}+\left({log}_{\mathrm{2}} \mathrm{5}\right)^{\mathrm{2}} \:}{\mathrm{2}+\:\mathrm{3}\:{log}_{\mathrm{2}} \:\mathrm{5}}\:\: \\ $$$$=\frac{\mathrm{10}\:+\mathrm{2}\left(\mathrm{2}.\mathrm{3219}\right)+\left(\mathrm{2}.\mathrm{3219}\right)^{\mathrm{2}} \:}{\mathrm{2}+\:\mathrm{3}\left(\mathrm{2}.\mathrm{3219}\right)}\approx\mathrm{2}.\mathrm{2346} \\ $$

Commented by mathdanisur last updated on 05/Aug/21

Thank You Ser

$${Thank}\:{You}\:\mathrm{Ser} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com