
Question Number 149415 by abdurehime last updated on 05/Aug/21
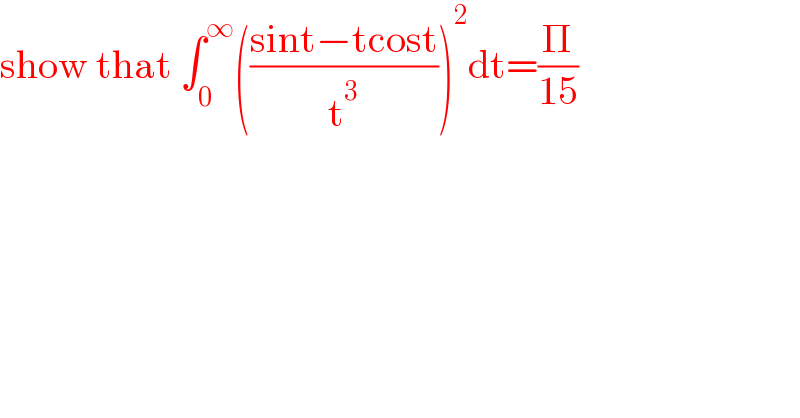
$$\mathrm{show}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{sint}−\mathrm{tcost}}{\mathrm{t}^{\mathrm{3}} }\right)^{\mathrm{2}} \mathrm{dt}=\frac{\Pi}{\mathrm{15}} \\ $$
Commented by abdurehime last updated on 05/Aug/21
$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}???? \\ $$
Answered by mindispower last updated on 05/Aug/21
![byart =[−(1/5)(((sin(t)−tcos(t))^2 )/(t^5 ))] +(2/5)∫_0 ^∞ (((sin(t)−tcos(t))sin(t))/t^4 )dt =(2/5)[(((sin(t)−tcos(t))sin(t))/(−3t^3 )) ]_0 ^∞ +(2/(15))∫_0 ^∞ (((sin(t)cos(t)−tcos(2t)))/t^3 )dt =(1/(15))[((sin(t)cos(t)−tcos(2t))/(−t^2 ))]_0 ^∞ +(1/(15))∫_0 ^∞ ((2tsin(2t))/t^2 ) =(1/(15))∫_0 ^∞ ((sin(2t).2dt)/t)=(2/(15))∫_0 ^∞ ((sin(x)dx)/x)=(2/(15)).(π/2)=(π/(15))](Q149432.png)
$${byart} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{5}}\frac{\left({sin}\left({t}\right)−{tcos}\left({t}\right)\right)^{\mathrm{2}} }{{t}^{\mathrm{5}} \:}\right] \\ $$$$+\frac{\mathrm{2}}{\mathrm{5}}\int_{\mathrm{0}} ^{\infty} \frac{\left({sin}\left({t}\right)−{tcos}\left({t}\right)\right){sin}\left({t}\right)}{{t}^{\mathrm{4}} }{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\left[\frac{\left({sin}\left({t}\right)−{tcos}\left({t}\right)\right){sin}\left({t}\right)}{−\mathrm{3}{t}^{\mathrm{3}} }\:\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{2}}{\mathrm{15}}\int_{\mathrm{0}} ^{\infty} \frac{\left({sin}\left({t}\right){cos}\left({t}\right)−{tcos}\left(\mathrm{2}{t}\right)\right)}{{t}^{\mathrm{3}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{15}}\left[\frac{{sin}\left({t}\right){cos}\left({t}\right)−{tcos}\left(\mathrm{2}{t}\right)}{−{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{15}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{tsin}\left(\mathrm{2}{t}\right)}{{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{15}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\mathrm{2}{t}\right).\mathrm{2}{dt}}{{t}}=\frac{\mathrm{2}}{\mathrm{15}}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right){dx}}{{x}}=\frac{\mathrm{2}}{\mathrm{15}}.\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{15}} \\ $$$$ \\ $$
Commented by abdurehime last updated on 05/Aug/21
$$\mathrm{please}\:\mathrm{show}\:\mathrm{me}\:\mathrm{step}\:\mathrm{by}\:\mathrm{step} \\ $$
Commented by mnjuly1970 last updated on 05/Aug/21
$$\:\:\:\:\:{very}\:{nice}\:{sir}\:{power}...{beavo}.. \\ $$
Commented by mindispower last updated on 05/Aug/21

$${thanx}\:{sir} \\ $$
