Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 149428 by mr W last updated on 06/Aug/21

Commented by mr W last updated on 06/Aug/21

three non−collinear points in space are given with coordinates A(x_1 ,y_1 ,z_1 ) B(x_2 ,y_2 ,z_2 ) C(x_3 ,y_3 ,z_3 ) find the coordinates of the center S and the radius R of the circumcircle.

$${three}\:{non}−{collinear}\:{points}\:{in}\:{space}\: \\ $$$${are}\:{given}\:{with}\:{coordinates} \\ $$$${A}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right) \\ $$$${B}\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} ,{z}_{\mathrm{2}} \right) \\ $$$${C}\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} ,{z}_{\mathrm{3}} \right) \\ $$$${find}\:{the}\:{coordinates}\:{of}\:{the}\:{center}\:{S} \\ $$$${and}\:{the}\:{radius}\:{R}\:{of}\:{the}\:{circumcircle}. \\ $$

Commented by ajfour last updated on 06/Aug/21

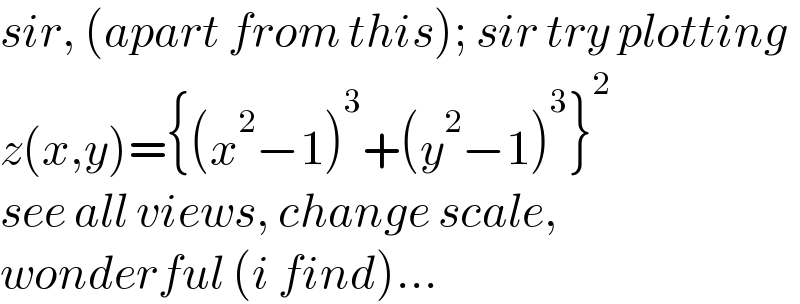
sir, (apart from this); sir try plotting z(x,y)={(x^2 −1)^3 +(y^2 −1)^3 }^2 see all views, change scale, wonderful (i find)...

$${sir},\:\left({apart}\:{from}\:{this}\right);\:{sir}\:{try}\:{plotting} \\ $$$${z}\left({x},{y}\right)=\left\{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} +\left({y}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} \right\}^{\mathrm{2}} \\ $$$${see}\:{all}\:{views},\:{change}\:{scale}, \\ $$$${wonderful}\:\left({i}\:{find}\right)... \\ $$

Commented by ajfour last updated on 06/Aug/21

Answered by ajfour last updated on 06/Aug/21

A(a), B(b), C(c) plane ABC (s−a).((b−c)×(a−c))=0 let S(s). n^� =(((b−c)×(a−c))/(∣(b−c)×(a−c)∣)) let s=(((b+c))/2)+((∣b−c∣)/(2tan A)){((n^� ×(b−c))/( ∣b−c∣))} ∣s−a∣=∣s−b∣=∣s−c∣=R

$${A}\left({a}\right),\:{B}\left({b}\right),\:{C}\left({c}\right) \\ $$$${plane}\:{ABC} \\ $$$$\left({s}−{a}\right).\left(\left({b}−{c}\right)×\left({a}−{c}\right)\right)=\mathrm{0} \\ $$$${let}\:\:{S}\left({s}\right). \\ $$$$\hat {{n}}=\frac{\left({b}−{c}\right)×\left({a}−{c}\right)}{\mid\left({b}−{c}\right)×\left({a}−{c}\right)\mid} \\ $$$${let}\:\:{s}=\frac{\left({b}+{c}\right)}{\mathrm{2}}+\frac{\mid{b}−{c}\mid}{\mathrm{2tan}\:{A}}\left\{\frac{\hat {{n}}×\left({b}−{c}\right)}{\:\mid{b}−{c}\mid}\right\} \\ $$$$\mid{s}−{a}\mid=\mid{s}−{b}\mid=\mid{s}−{c}\mid={R} \\ $$

Commented by mr W last updated on 06/Aug/21

thanks sir! i′ll also try to use vectors.

$${thanks}\:{sir}!\:{i}'{ll}\:{also}\:{try}\:{to}\:{use}\:{vectors}. \\ $$

Commented by ajfour last updated on 06/Aug/21

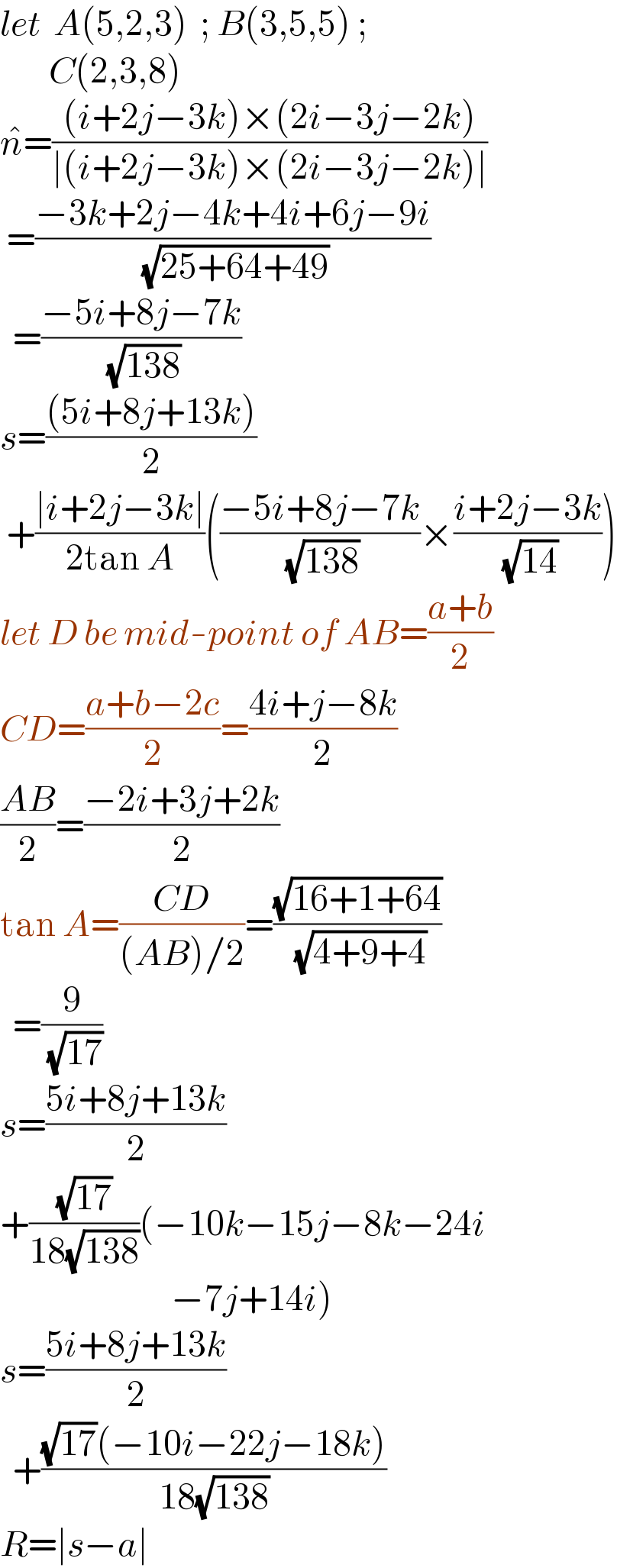
let A(5,2,3) ; B(3,5,5) ; C(2,3,8) n^� =(((i+2j−3k)×(2i−3j−2k))/(∣(i+2j−3k)×(2i−3j−2k)∣)) =((−3k+2j−4k+4i+6j−9i)/( (√(25+64+49)))) =((−5i+8j−7k)/( (√(138)))) s=(((5i+8j+13k))/2) +((∣i+2j−3k∣)/(2tan A))(((−5i+8j−7k)/( (√(138))))×((i+2j−3k)/( (√(14))))) let D be mid-point of AB=((a+b)/2) CD=((a+b−2c)/2)=((4i+j−8k)/2) ((AB)/2)=((−2i+3j+2k)/2) tan A=((CD)/((AB)/2))=((√(16+1+64))/( (√(4+9+4)))) =(9/( (√(17)))) s=((5i+8j+13k)/2) +((√(17))/(18(√(138))))(−10k−15j−8k−24i −7j+14i) s=((5i+8j+13k)/2) +(((√(17))(−10i−22j−18k))/(18(√(138)))) R=∣s−a∣

$${let}\:\:{A}\left(\mathrm{5},\mathrm{2},\mathrm{3}\right)\:\:;\:{B}\left(\mathrm{3},\mathrm{5},\mathrm{5}\right)\:;\: \\ $$$$\:\:\:\:\:\:\:\:{C}\left(\mathrm{2},\mathrm{3},\mathrm{8}\right) \\ $$$$\hat {{n}}=\frac{\left({i}+\mathrm{2}{j}−\mathrm{3}{k}\right)×\left(\mathrm{2}{i}−\mathrm{3}{j}−\mathrm{2}{k}\right)}{\mid\left({i}+\mathrm{2}{j}−\mathrm{3}{k}\right)×\left(\mathrm{2}{i}−\mathrm{3}{j}−\mathrm{2}{k}\right)\mid} \\ $$$$\:=\frac{−\mathrm{3}{k}+\mathrm{2}{j}−\mathrm{4}{k}+\mathrm{4}{i}+\mathrm{6}{j}−\mathrm{9}{i}}{\:\sqrt{\mathrm{25}+\mathrm{64}+\mathrm{49}}} \\ $$$$\:\:=\frac{−\mathrm{5}{i}+\mathrm{8}{j}−\mathrm{7}{k}}{\:\sqrt{\mathrm{138}}} \\ $$$${s}=\frac{\left(\mathrm{5}{i}+\mathrm{8}{j}+\mathrm{13}{k}\right)}{\mathrm{2}} \\ $$$$\:+\frac{\mid{i}+\mathrm{2}{j}−\mathrm{3}{k}\mid}{\mathrm{2tan}\:{A}}\left(\frac{−\mathrm{5}{i}+\mathrm{8}{j}−\mathrm{7}{k}}{\:\sqrt{\mathrm{138}}}×\frac{{i}+\mathrm{2}{j}−\mathrm{3}{k}}{\:\sqrt{\mathrm{14}}}\right) \\ $$$${let}\:{D}\:{be}\:{mid}-{point}\:{of}\:{AB}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$${CD}=\frac{{a}+{b}−\mathrm{2}{c}}{\mathrm{2}}=\frac{\mathrm{4}{i}+{j}−\mathrm{8}{k}}{\mathrm{2}} \\ $$$$\frac{{AB}}{\mathrm{2}}=\frac{−\mathrm{2}{i}+\mathrm{3}{j}+\mathrm{2}{k}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:{A}=\frac{{CD}}{\left({AB}\right)/\mathrm{2}}=\frac{\sqrt{\mathrm{16}+\mathrm{1}+\mathrm{64}}}{\:\sqrt{\mathrm{4}+\mathrm{9}+\mathrm{4}}} \\ $$$$\:\:=\frac{\mathrm{9}}{\:\sqrt{\mathrm{17}}} \\ $$$${s}=\frac{\mathrm{5}{i}+\mathrm{8}{j}+\mathrm{13}{k}}{\mathrm{2}} \\ $$$$+\frac{\sqrt{\mathrm{17}}}{\mathrm{18}\sqrt{\mathrm{138}}}\left(−\mathrm{10}{k}−\mathrm{15}{j}−\mathrm{8}{k}−\mathrm{24}{i}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{7}{j}+\mathrm{14}{i}\right) \\ $$$${s}=\frac{\mathrm{5}{i}+\mathrm{8}{j}+\mathrm{13}{k}}{\mathrm{2}} \\ $$$$\:\:+\frac{\sqrt{\mathrm{17}}\left(−\mathrm{10}{i}−\mathrm{22}{j}−\mathrm{18}{k}\right)}{\mathrm{18}\sqrt{\mathrm{138}}} \\ $$$${R}=\mid{s}−{a}\mid \\ $$

Commented by mr W last updated on 07/Aug/21

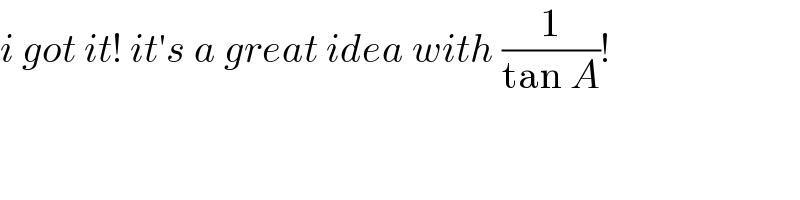
i got it! it′s a great idea with (1/(tan A))!

$${i}\:{got}\:{it}!\:{it}'{s}\:{a}\:{great}\:{idea}\:{with}\:\frac{\mathrm{1}}{\mathrm{tan}\:{A}}! \\ $$

Commented by ajfour last updated on 07/Aug/21

Answered by mr W last updated on 07/Aug/21

Commented by mr W last updated on 07/Aug/21

let a=OA^(→) , b=OB^(→) , c=OC^(→) , s=OS^(→) let p=AB^(→) , q=BC^(→) , r=CA^(→) normal of plane ABC: n=((r×q)/(∣r×q∣)) D=midpoint of AB OD^(→) =((a+b)/2) ∣DS^(→) ∣=((∣AB^(→) ∣)/2)tan φ=((∣p∣)/(2 tan ∠C)) DS^(→) =∣DS^(→) ∣((p×n)/(∣p∣))=((∣p∣)/(2 tan ∠C))×((p×(r×q))/(∣p∣∣r×q∣)) DS^(→) =(1/(tan ∠C))×((p×(r×q))/(2∣r×q∣)) s=OD^(→) +DS^(→) s=((a+b)/2)+(1/(tan ∠C))×((p×(r×q))/(2∣r×q∣)) cos C=−((q∙r)/(∣q∣∣r∣)) sin C=((∣q×r∣)/(∣q∣∣r∣)) (1/(tan C))=−((q∙r)/(∣q×r∣)) s=((a+b)/2)−((q∙r)/(∣q×r∣))×((p×(r×q))/(2∣r×q∣)) ⇒s=(1/2){a+b+((q∙r)/(∣q×r∣^2 )) p×(q×r)} ⇒R=∣s−a∣=∣s−b∣=∣s−c∣ or R=((∣p∣)/(2 sin ∠C))=((∣p∣∣q∣∣r∣)/(2∣q×r∣)) example: A(5,2,3), B(3,5,5), C(2,3,8) p=(−2,3,2) q=(−1,−2,3) r=(3,−1,−5) q∙r=−3+2−15=−16 q×r= determinant (((−1),(−2),3),(3,(−1),(−5)))=(13,4,7) ∣q×r∣^2 =13^2 +4^2 +7^2 =234 p×(q×r)= determinant (((−2),3,2),((13),4,7))=(13,40,−47) s=(1/2){(5,2,3)+(3,5,5)−((16)/(234))(13,40,−47)} =(((32)/9),((499)/(234)),((656)/(117))) R^2 =∣AS^(→) ∣^2 =(((32)/9)−5)^2 +(((499)/(234))−2)^2 +(((656)/(117))−3)^2 =((4165)/(468)) ✓ R^2 =∣BS^(→) ∣^2 =(((32)/9)−3)^2 +(((499)/(234))−5)^2 +(((656)/(117))−5)^2 =((4165)/(468)) ✓ R^2 =∣CS^(→) ∣^2 =(((32)/9)−2)^2 +(((499)/(234))−3)^2 +(((656)/(117))−8)^2 =((4165)/(468)) ✓ R=(√((4165)/(468)))=((7(√(1105)))/(78))

$${let}\:\boldsymbol{{a}}=\overset{\rightarrow} {\boldsymbol{{OA}}},\:\boldsymbol{{b}}=\overset{\rightarrow} {\boldsymbol{{OB}}},\:\boldsymbol{{c}}=\overset{\rightarrow} {\boldsymbol{{OC}}},\:\boldsymbol{{s}}=\overset{\rightarrow} {\boldsymbol{{OS}}} \\ $$$${let}\:\boldsymbol{{p}}=\overset{\rightarrow} {\boldsymbol{{AB}}},\:\boldsymbol{{q}}=\overset{\rightarrow} {\boldsymbol{{BC}}},\:\boldsymbol{{r}}=\overset{\rightarrow} {\boldsymbol{{CA}}} \\ $$$${normal}\:{of}\:{plane}\:{ABC}: \\ $$$$\boldsymbol{{n}}=\frac{\boldsymbol{{r}}×\boldsymbol{{q}}}{\mid\boldsymbol{{r}}×\boldsymbol{{q}}\mid} \\ $$$${D}={midpoint}\:{of}\:{AB} \\ $$$$\overset{\rightarrow} {\boldsymbol{{OD}}}=\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\mathrm{2}} \\ $$$$\mid\overset{\rightarrow} {\boldsymbol{{DS}}}\mid=\frac{\mid\overset{\rightarrow} {\boldsymbol{{AB}}}\mid}{\mathrm{2}}\mathrm{tan}\:\phi=\frac{\mid\boldsymbol{{p}}\mid}{\mathrm{2}\:\mathrm{tan}\:\angle{C}} \\ $$$$\overset{\rightarrow} {\boldsymbol{{DS}}}=\mid\overset{\rightarrow} {\boldsymbol{{DS}}}\mid\frac{\boldsymbol{{p}}×\boldsymbol{{n}}}{\mid\boldsymbol{{p}}\mid}=\frac{\mid\boldsymbol{{p}}\mid}{\mathrm{2}\:\mathrm{tan}\:\angle{C}}×\frac{\boldsymbol{{p}}×\left(\boldsymbol{{r}}×\boldsymbol{{q}}\right)}{\mid\boldsymbol{{p}}\mid\mid\boldsymbol{{r}}×\boldsymbol{{q}}\mid} \\ $$$$\overset{\rightarrow} {\boldsymbol{{DS}}}=\frac{\mathrm{1}}{\mathrm{tan}\:\angle{C}}×\frac{\boldsymbol{{p}}×\left(\boldsymbol{{r}}×\boldsymbol{{q}}\right)}{\mathrm{2}\mid\boldsymbol{{r}}×\boldsymbol{{q}}\mid} \\ $$$$\boldsymbol{{s}}=\overset{\rightarrow} {\boldsymbol{{OD}}}+\overset{\rightarrow} {\boldsymbol{{DS}}} \\ $$$$\boldsymbol{{s}}=\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{tan}\:\angle{C}}×\frac{\boldsymbol{{p}}×\left(\boldsymbol{{r}}×\boldsymbol{{q}}\right)}{\mathrm{2}\mid\boldsymbol{{r}}×\boldsymbol{{q}}\mid} \\ $$$$\mathrm{cos}\:{C}=−\frac{\boldsymbol{{q}}\centerdot\boldsymbol{{r}}}{\mid\boldsymbol{{q}}\mid\mid\boldsymbol{{r}}\mid} \\ $$$$\mathrm{sin}\:{C}=\frac{\mid\boldsymbol{{q}}×\boldsymbol{{r}}\mid}{\mid\boldsymbol{{q}}\mid\mid\boldsymbol{{r}}\mid} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:{C}}=−\frac{\boldsymbol{{q}}\centerdot\boldsymbol{{r}}}{\mid\boldsymbol{{q}}×\boldsymbol{{r}}\mid} \\ $$$$\boldsymbol{{s}}=\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\mathrm{2}}−\frac{\boldsymbol{{q}}\centerdot\boldsymbol{{r}}}{\mid\boldsymbol{{q}}×\boldsymbol{{r}}\mid}×\frac{\boldsymbol{{p}}×\left(\boldsymbol{{r}}×\boldsymbol{{q}}\right)}{\mathrm{2}\mid\boldsymbol{{r}}×\boldsymbol{{q}}\mid} \\ $$$$\Rightarrow\boldsymbol{{s}}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\boldsymbol{{a}}+\boldsymbol{{b}}+\frac{\boldsymbol{{q}}\centerdot\boldsymbol{{r}}}{\mid\boldsymbol{{q}}×\boldsymbol{{r}}\mid^{\mathrm{2}} }\:\boldsymbol{{p}}×\left(\boldsymbol{{q}}×\boldsymbol{{r}}\right)\right\} \\ $$$$\Rightarrow{R}=\mid\boldsymbol{{s}}−\boldsymbol{{a}}\mid=\mid\boldsymbol{{s}}−\boldsymbol{{b}}\mid=\mid\boldsymbol{{s}}−\boldsymbol{{c}}\mid \\ $$$${or}\:{R}=\frac{\mid\boldsymbol{{p}}\mid}{\mathrm{2}\:\mathrm{sin}\:\angle{C}}=\frac{\mid\boldsymbol{{p}}\mid\mid\boldsymbol{{q}}\mid\mid\boldsymbol{{r}}\mid}{\mathrm{2}\mid\boldsymbol{{q}}×\boldsymbol{{r}}\mid} \\ $$$$ \\ $$$${example}: \\ $$$${A}\left(\mathrm{5},\mathrm{2},\mathrm{3}\right),\:{B}\left(\mathrm{3},\mathrm{5},\mathrm{5}\right),\:{C}\left(\mathrm{2},\mathrm{3},\mathrm{8}\right) \\ $$$${p}=\left(−\mathrm{2},\mathrm{3},\mathrm{2}\right) \\ $$$${q}=\left(−\mathrm{1},−\mathrm{2},\mathrm{3}\right) \\ $$$${r}=\left(\mathrm{3},−\mathrm{1},−\mathrm{5}\right) \\ $$$${q}\centerdot{r}=−\mathrm{3}+\mathrm{2}−\mathrm{15}=−\mathrm{16} \\ $$$${q}×{r}=\begin{vmatrix}{−\mathrm{1}}&{−\mathrm{2}}&{\mathrm{3}}\\{\mathrm{3}}&{−\mathrm{1}}&{−\mathrm{5}}\end{vmatrix}=\left(\mathrm{13},\mathrm{4},\mathrm{7}\right) \\ $$$$\mid{q}×{r}\mid^{\mathrm{2}} =\mathrm{13}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} =\mathrm{234} \\ $$$${p}×\left({q}×{r}\right)=\begin{vmatrix}{−\mathrm{2}}&{\mathrm{3}}&{\mathrm{2}}\\{\mathrm{13}}&{\mathrm{4}}&{\mathrm{7}}\end{vmatrix}=\left(\mathrm{13},\mathrm{40},−\mathrm{47}\right) \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{5},\mathrm{2},\mathrm{3}\right)+\left(\mathrm{3},\mathrm{5},\mathrm{5}\right)−\frac{\mathrm{16}}{\mathrm{234}}\left(\mathrm{13},\mathrm{40},−\mathrm{47}\right)\right\} \\ $$$$\:\:=\left(\frac{\mathrm{32}}{\mathrm{9}},\frac{\mathrm{499}}{\mathrm{234}},\frac{\mathrm{656}}{\mathrm{117}}\right) \\ $$$${R}^{\mathrm{2}} =\mid\overset{\rightarrow} {\boldsymbol{{AS}}}\mid^{\mathrm{2}} =\left(\frac{\mathrm{32}}{\mathrm{9}}−\mathrm{5}\right)^{\mathrm{2}} +\left(\frac{\mathrm{499}}{\mathrm{234}}−\mathrm{2}\right)^{\mathrm{2}} +\left(\frac{\mathrm{656}}{\mathrm{117}}−\mathrm{3}\right)^{\mathrm{2}} =\frac{\mathrm{4165}}{\mathrm{468}}\:\checkmark \\ $$$${R}^{\mathrm{2}} =\mid\overset{\rightarrow} {\boldsymbol{{BS}}}\mid^{\mathrm{2}} =\left(\frac{\mathrm{32}}{\mathrm{9}}−\mathrm{3}\right)^{\mathrm{2}} +\left(\frac{\mathrm{499}}{\mathrm{234}}−\mathrm{5}\right)^{\mathrm{2}} +\left(\frac{\mathrm{656}}{\mathrm{117}}−\mathrm{5}\right)^{\mathrm{2}} =\frac{\mathrm{4165}}{\mathrm{468}}\:\checkmark \\ $$$${R}^{\mathrm{2}} =\mid\overset{\rightarrow} {\boldsymbol{{CS}}}\mid^{\mathrm{2}} =\left(\frac{\mathrm{32}}{\mathrm{9}}−\mathrm{2}\right)^{\mathrm{2}} +\left(\frac{\mathrm{499}}{\mathrm{234}}−\mathrm{3}\right)^{\mathrm{2}} +\left(\frac{\mathrm{656}}{\mathrm{117}}−\mathrm{8}\right)^{\mathrm{2}} =\frac{\mathrm{4165}}{\mathrm{468}}\:\checkmark \\ $$$${R}=\sqrt{\frac{\mathrm{4165}}{\mathrm{468}}}=\frac{\mathrm{7}\sqrt{\mathrm{1105}}}{\mathrm{78}} \\ $$

Commented by mr W last updated on 07/Aug/21

a special case A(u,0,0) B(0,v,0) C(0,0,w) p=(−u,v,0) q=(0,−v,w) r=(u,0,−w) q∙r=−w^2 q×r= determinant ((0,(−v),w),(u,0,(−w)))=(vw,wu,uv) ∣q×r∣^2 =u^2 v^2 +v^2 w^2 +w^2 u^2 p×(q×r)= determinant (((−u),v,0),((vw),(wu),(uv)))=(uv^2 ,u^2 v,−w(u^2 +v^2 )) s=(1/2){(u,0,0)+(0,v,0)−(w^2 /(u^2 v^2 +v^2 w^2 +w^2 u^2 )) (uv^2 ,u^2 v,−w(u^2 +v^2 ))} =(1/2){u−((uv^2 w^2 )/(u^2 v^2 +v^2 w^2 +w^2 u^2 )),v−((u^2 vw^2 )/(u^2 v^2 +v^2 w^2 +w^2 u^2 )),((w^3 (u^2 +v^2 ))/(u^2 v^2 +v^2 w^2 +w^2 u^2 ))} =(1/2){((u^3 (v^2 +w^2 ))/(u^2 v^2 +v^2 w^2 +w^2 u^2 )),((v^3 (w^2 +u^2 ))/(u^2 v^2 +v^2 w^2 +w^2 u^2 )),((w^3 (u^2 +v^2 ))/(u^2 v^2 +v^2 w^2 +w^2 u^2 ))} ∣p∣=(√(u^2 +v^2 )) ∣q∣=(√(v^2 +w^2 )) ∣r∣=(√(w^2 +u^2 )) ∣q×r∣=(√(u^2 v^2 +v^2 w^2 +w^2 u^2 )) ⇒R=(1/2)(√(((u^2 +v^2 )(v^2 +w^2 )(w^2 +u^2 ))/(u^2 v^2 +v^2 w^2 +w^2 u^2 )))

$$\boldsymbol{{a}}\:\boldsymbol{{special}}\:\boldsymbol{{case}} \\ $$$${A}\left({u},\mathrm{0},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{0},{v},\mathrm{0}\right) \\ $$$${C}\left(\mathrm{0},\mathrm{0},{w}\right) \\ $$$${p}=\left(−{u},{v},\mathrm{0}\right) \\ $$$${q}=\left(\mathrm{0},−{v},{w}\right) \\ $$$${r}=\left({u},\mathrm{0},−{w}\right) \\ $$$${q}\centerdot{r}=−{w}^{\mathrm{2}} \\ $$$${q}×{r}=\begin{vmatrix}{\mathrm{0}}&{−{v}}&{{w}}\\{{u}}&{\mathrm{0}}&{−{w}}\end{vmatrix}=\left({vw},{wu},{uv}\right) \\ $$$$\mid{q}×{r}\mid^{\mathrm{2}} ={u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} \\ $$$${p}×\left({q}×{r}\right)=\begin{vmatrix}{−{u}}&{{v}}&{\mathrm{0}}\\{{vw}}&{{wu}}&{{uv}}\end{vmatrix}=\left({uv}^{\mathrm{2}} ,{u}^{\mathrm{2}} {v},−{w}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\right) \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left({u},\mathrm{0},\mathrm{0}\right)+\left(\mathrm{0},{v},\mathrm{0}\right)−\frac{{w}^{\mathrm{2}} }{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} }\:\left({uv}^{\mathrm{2}} ,{u}^{\mathrm{2}} {v},−{w}\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{u}−\frac{{uv}^{\mathrm{2}} {w}^{\mathrm{2}} }{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} },{v}−\frac{{u}^{\mathrm{2}} {vw}^{\mathrm{2}} }{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} },\frac{{w}^{\mathrm{3}} \left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{u}^{\mathrm{3}} \left({v}^{\mathrm{2}} +{w}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} },\frac{{v}^{\mathrm{3}} \left({w}^{\mathrm{2}} +{u}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} },\frac{{w}^{\mathrm{3}} \left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} }\right\} \\ $$$$ \\ $$$$\mid{p}\mid=\sqrt{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} } \\ $$$$\mid{q}\mid=\sqrt{{v}^{\mathrm{2}} +{w}^{\mathrm{2}} } \\ $$$$\mid{r}\mid=\sqrt{{w}^{\mathrm{2}} +{u}^{\mathrm{2}} } \\ $$$$\mid{q}×{r}\mid=\sqrt{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} } \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)\left({v}^{\mathrm{2}} +{w}^{\mathrm{2}} \right)\left({w}^{\mathrm{2}} +{u}^{\mathrm{2}} \right)}{{u}^{\mathrm{2}} {v}^{\mathrm{2}} +{v}^{\mathrm{2}} {w}^{\mathrm{2}} +{w}^{\mathrm{2}} {u}^{\mathrm{2}} }} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com