Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 149505 by mathdanisur last updated on 05/Aug/21

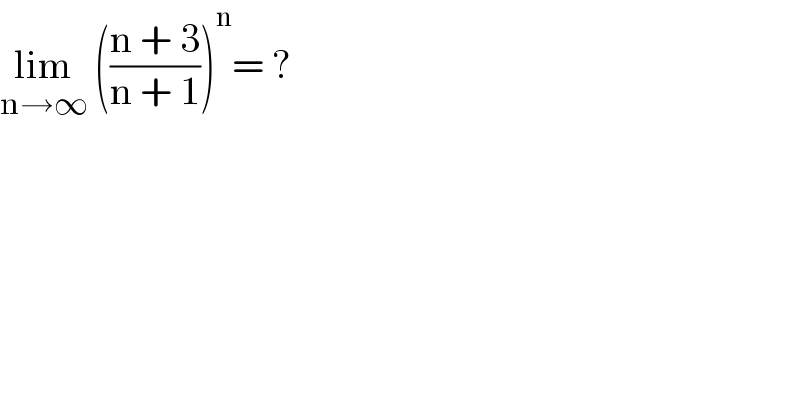
lim_(n→∞) (((n + 3)/(n + 1)))^n = ?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{n}\:+\:\mathrm{3}}{\mathrm{n}\:+\:\mathrm{1}}\right)^{\mathrm{n}} =\:? \\ $$

Commented by EDWIN88 last updated on 06/Aug/21

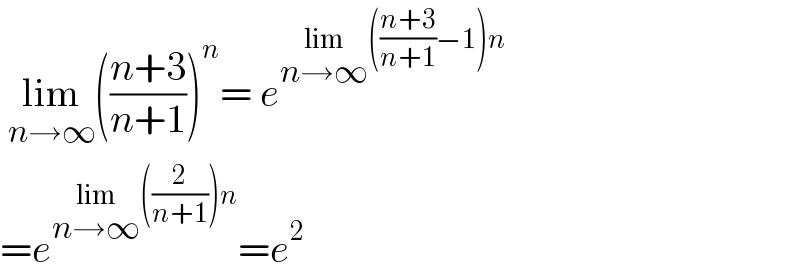
lim_(n→∞) (((n+3)/(n+1)))^n = e^(lim_(n→∞) (((n+3)/(n+1))−1)n) =e^(lim_(n→∞) ((2/(n+1)))n) =e^2

$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}+\mathrm{3}}{{n}+\mathrm{1}}\right)^{{n}} =\:{e}^{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}+\mathrm{3}}{{n}+\mathrm{1}}−\mathrm{1}\right){n}} \\ $$$$={e}^{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}}{{n}+\mathrm{1}}\right){n}} ={e}^{\mathrm{2}} \\ $$

Commented by mathdanisur last updated on 06/Aug/21

Thankyou Ser

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$

Answered by Ar Brandon last updated on 06/Aug/21

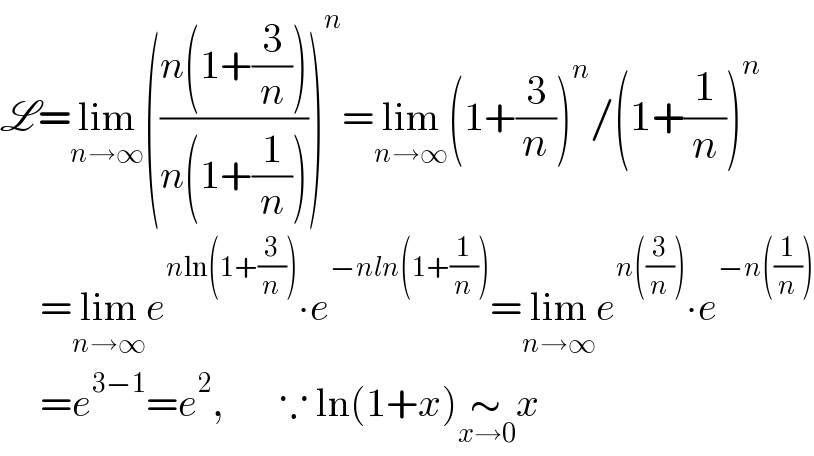
L=lim_(n→∞) (((n(1+(3/n)))/(n(1+(1/n)))))^n =lim_(n→∞) (1+(3/n))^n /(1+(1/n))^n =lim_(n→∞) e^(nln(1+(3/n))) ∙e^(−nln(1+(1/n))) =lim_(n→∞) e^(n((3/n))) ∙e^(−n((1/n))) =e^(3−1) =e^2 , ∵ ln(1+x)∼_(x→0) x

$$\mathscr{L}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)}{{n}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)}\right)^{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{{n}} /\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \\ $$$$\:\:\:\:\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{e}^{{n}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)} \centerdot{e}^{−{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}{e}^{{n}\left(\frac{\mathrm{3}}{{n}}\right)} \centerdot{e}^{−{n}\left(\frac{\mathrm{1}}{{n}}\right)} \\ $$$$\:\:\:\:\:={e}^{\mathrm{3}−\mathrm{1}} ={e}^{\mathrm{2}} ,\:\:\:\:\:\:\:\because\:\mathrm{ln}\left(\mathrm{1}+{x}\right)\underset{{x}\rightarrow\mathrm{0}} {\sim}{x} \\ $$

Commented by mathdanisur last updated on 05/Aug/21

Ser, thank you

$$\boldsymbol{\mathrm{Ser}},\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by mindispower last updated on 06/Aug/21

(1+(a/n))^n →e^a

$$\left(\mathrm{1}+\frac{{a}}{{n}}\right)^{{n}} \rightarrow{e}^{{a}} \\ $$

Commented by Ar Brandon last updated on 06/Aug/21

Oh thanks !

$$\mathrm{Oh}\:\mathrm{thanks}\:! \\ $$

Commented by mathdanisur last updated on 06/Aug/21

Thankyou Ser

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$

Answered by ArielVyny last updated on 06/Aug/21

lim[((n(1+(3/n)))/(n(1+(1/n))))]^n =lim(((1+(3/n))^n )/((1+(1/n))^n ))=(e^(nln(1+(3/n))) /e^(nln(1+(1/n))) )=(e^3 /e^1 )=e^2

$${lim}\left[\frac{{n}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)}{{n}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)}\right]^{{n}} ={lim}\frac{\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{{n}} }{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} }=\frac{{e}^{{nln}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)} }{{e}^{{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} }=\frac{{e}^{\mathrm{3}} }{{e}^{\mathrm{1}} }={e}^{\mathrm{2}} \\ $$

Commented by mathdanisur last updated on 06/Aug/21

Thankyou Ser

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$

Answered by Olaf_Thorendsen last updated on 06/Aug/21

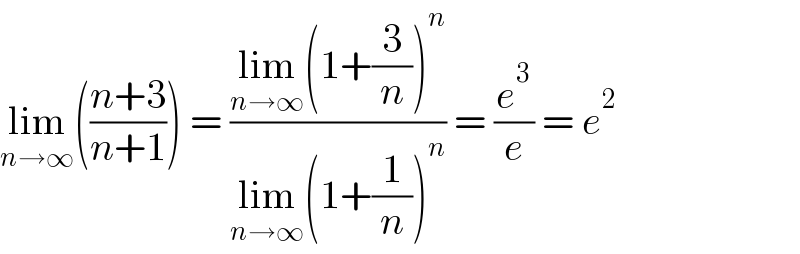
lim_(n→∞) (((n+3)/(n+1))) = ((lim_(n→∞) (1+(3/n))^n )/(lim_(n→∞) (1+(1/n))^n )) = (e^3 /e) = e^2

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}+\mathrm{3}}{{n}+\mathrm{1}}\right)\:=\:\frac{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{3}}{{n}}\right)^{{n}} }{\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} }\:=\:\frac{{e}^{\mathrm{3}} }{{e}}\:=\:{e}^{\mathrm{2}} \\ $$

Commented by mathdanisur last updated on 06/Aug/21

Thankyou Ser

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com