Question Number 149588 by mathdanisur last updated on 06/Aug/21

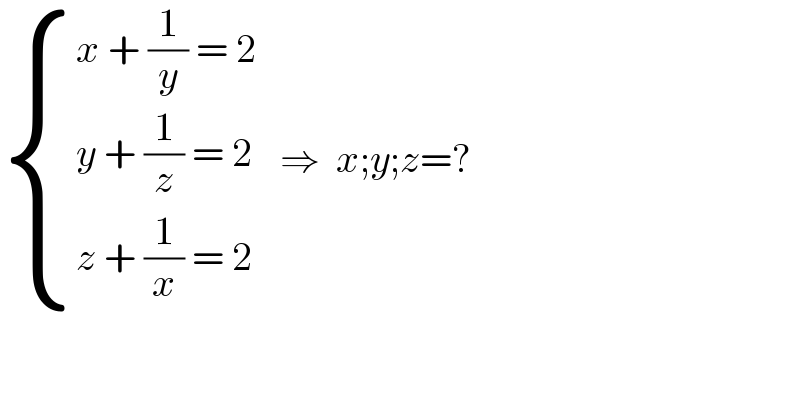
{ ((x + (1/y) = 2)),((y + (1/z) = 2)),((z + (1/x) = 2)) :} ⇒ x;y;z=?

Commented byAr Brandon last updated on 06/Aug/21

1;1;1

Commented bymathdanisur last updated on 06/Aug/21

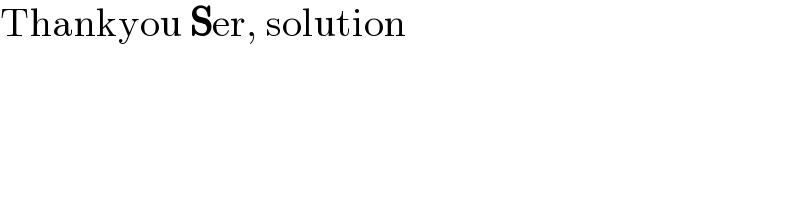
Thankyou Ser, solution

Answered by iloveisrael last updated on 06/Aug/21

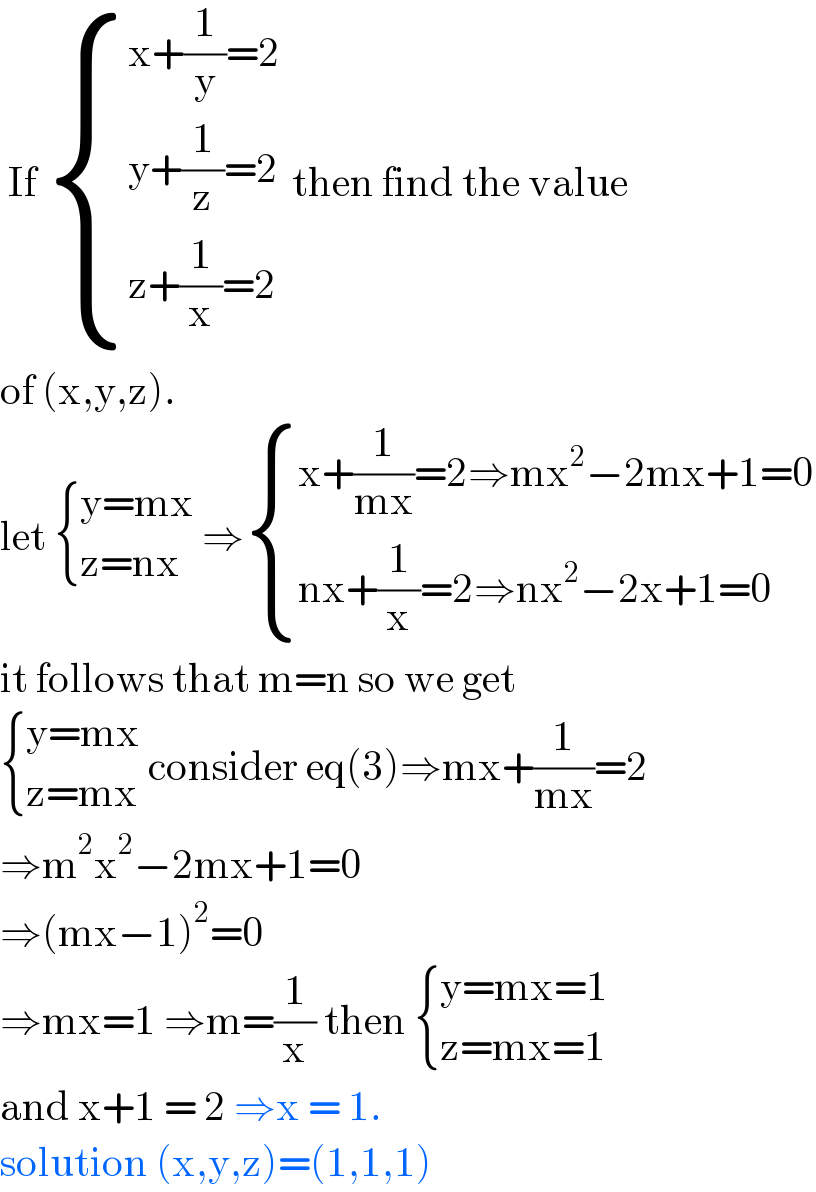
If { ((x+(1/y)=2)),((y+(1/z)=2)),((z+(1/x)=2 )) :} then find the value of (x,y,z). let { ((y=mx)),((z=nx)) :} ⇒ { ((x+(1/(mx))=2⇒mx^2 −2mx+1=0)),((nx+(1/x)=2⇒nx^2 −2x+1=0)) :} it follows that m=n so we get { ((y=mx)),((z=mx)) :} consider eq(3)⇒mx+(1/(mx))=2 ⇒m^2 x^2 −2mx+1=0 ⇒(mx−1)^2 =0 ⇒mx=1 ⇒m=(1/x) then { ((y=mx=1)),((z=mx=1)) :} and x+1 = 2 ⇒x = 1. solution (x,y,z)=(1,1,1)

Commented byRasheed.Sindhi last updated on 07/Aug/21

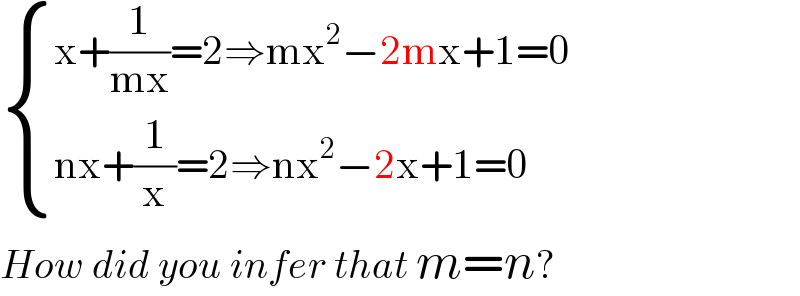
{ ((x+(1/(mx))=2⇒mx^2 −2mx+1=0)),((nx+(1/x)=2⇒nx^2 −2x+1=0)) :} How did you infer that m=n?

Commented byRasheed.Sindhi last updated on 07/Aug/21

Thank you!

Commented byiloveisrael last updated on 07/Aug/21

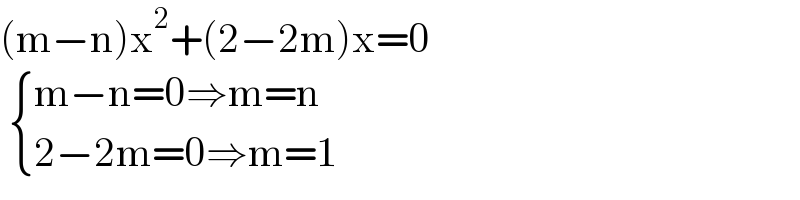
(m−n)x^2 +(2−2m)x=0 { ((m−n=0⇒m=n)),((2−2m=0⇒m=1)) :}

Commented bymathdanisur last updated on 06/Aug/21

Ser, thank you

Answered by Rasheed.Sindhi last updated on 06/Aug/21

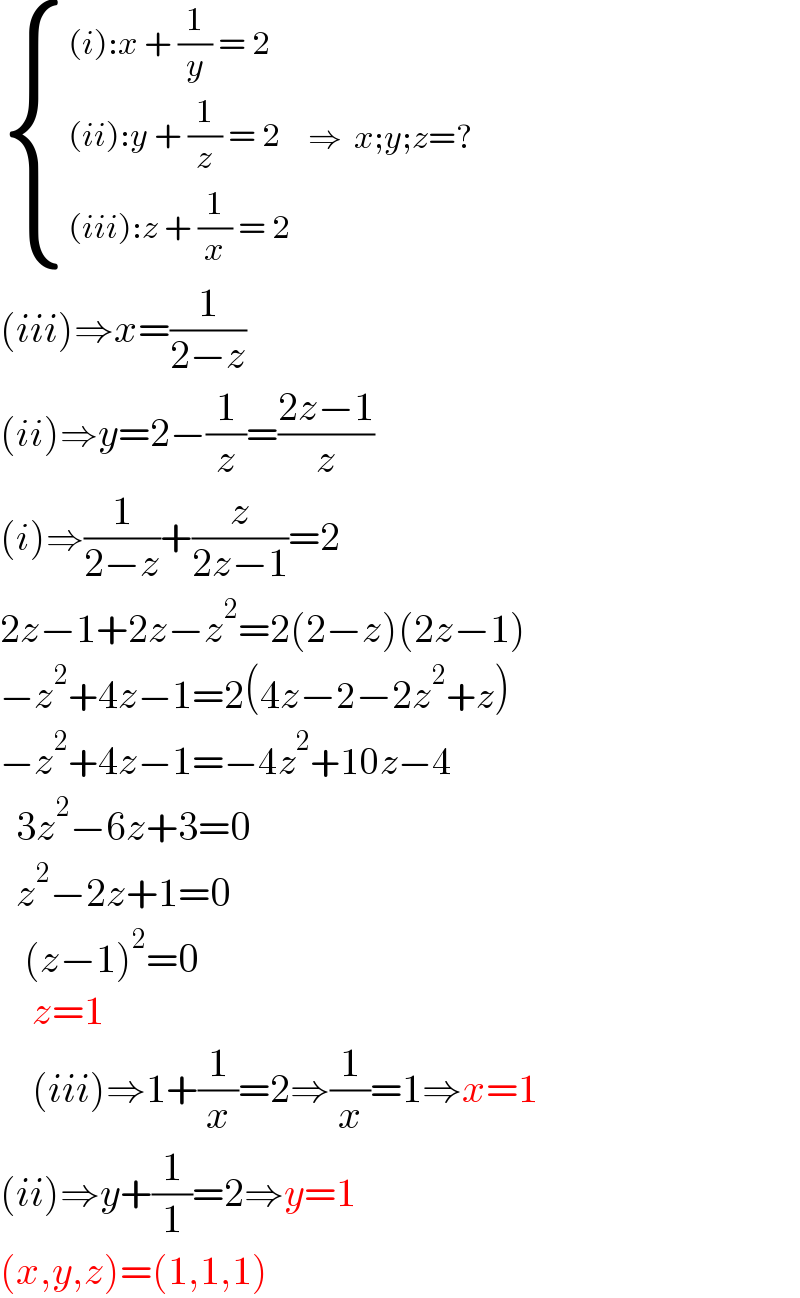
{ (((i):x + (1/y) = 2)),(((ii):y + (1/z) = 2)),(((iii):z + (1/x) = 2)) :} ⇒ x;y;z=? (iii)⇒x=(1/(2−z)) (ii)⇒y=2−(1/z)=((2z−1)/z) (i)⇒(1/(2−z))+(z/(2z−1))=2 2z−1+2z−z^2 =2(2−z)(2z−1) −z^2 +4z−1=2(4z−2−2z^2 +z) −z^2 +4z−1=−4z^2 +10z−4 3z^2 −6z+3=0 z^2 −2z+1=0 (z−1)^2 =0 z=1 (iii)⇒1+(1/x)=2⇒(1/x)=1⇒x=1 (ii)⇒y+(1/1)=2⇒y=1 (x,y,z)=(1,1,1)

Commented bymathdanisur last updated on 07/Aug/21

Thank you Ser