Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 149608 by puissant last updated on 06/Aug/21

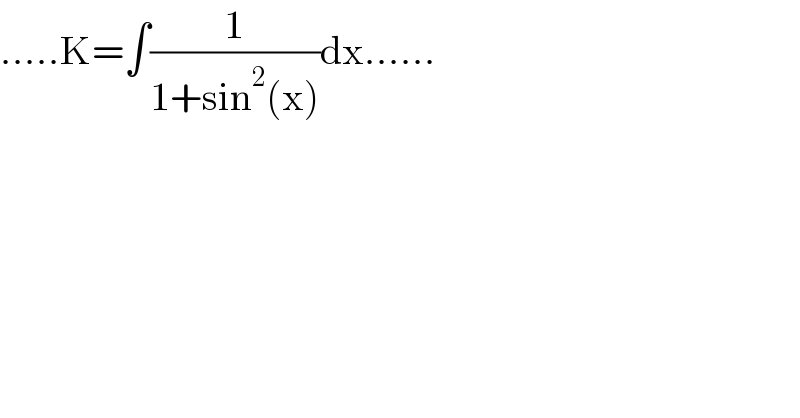
.....K=∫(1/(1+sin^2 (x)))dx......

$$.....\mathrm{K}=\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx}...... \\ $$

Answered by ArielVyny last updated on 06/Aug/21

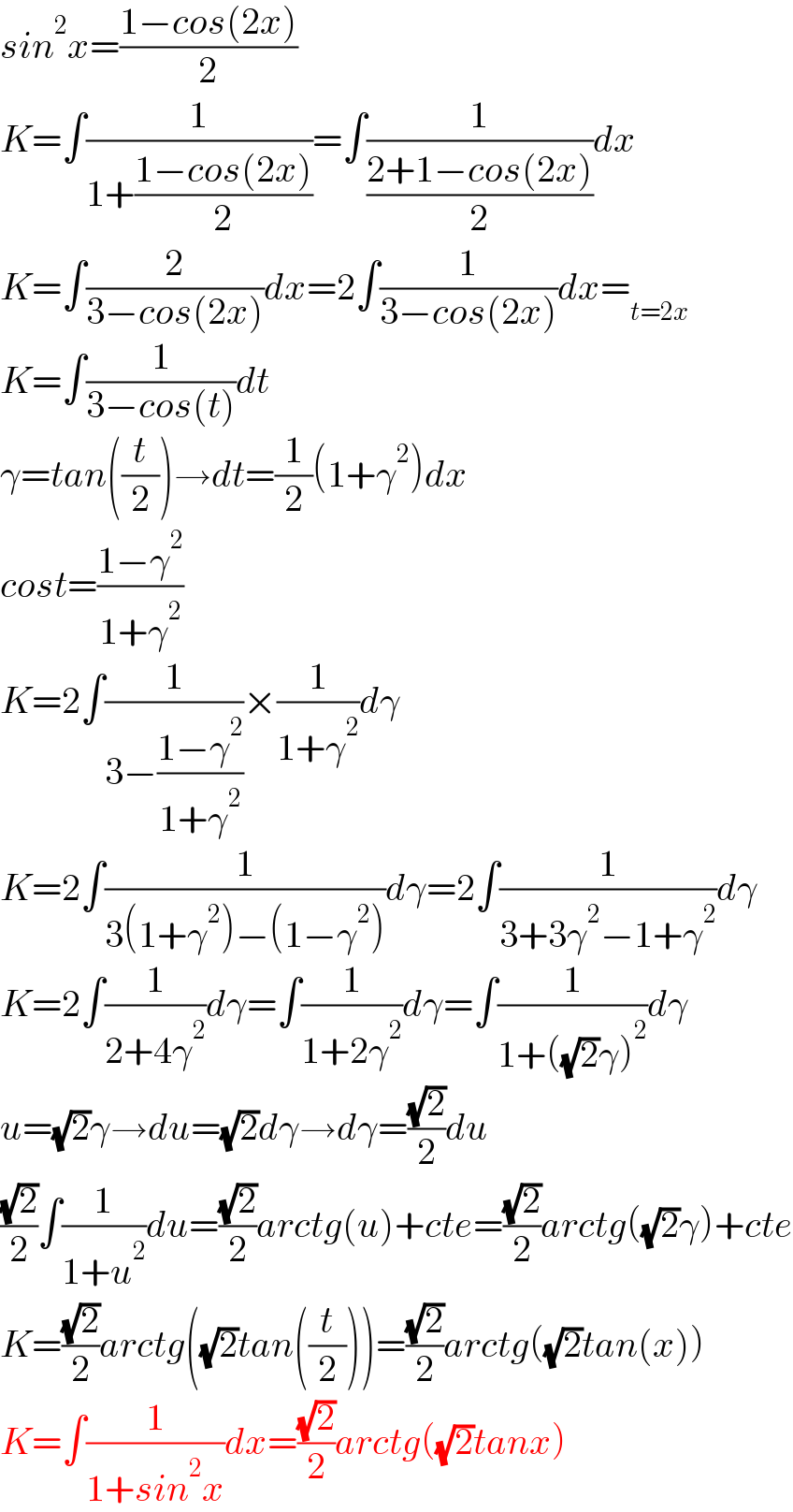
sin^2 x=((1−cos(2x))/2) K=∫(1/(1+((1−cos(2x))/2)))=∫(1/((2+1−cos(2x))/2))dx K=∫(2/(3−cos(2x)))dx=2∫(1/(3−cos(2x)))dx=_(t=2x) K=∫(1/(3−cos(t)))dt γ=tan((t/2))→dt=(1/2)(1+γ^2 )dx cost=((1−γ^2 )/(1+γ^2 )) K=2∫(1/(3−((1−γ^2 )/(1+γ^2 ))))×(1/(1+γ^2 ))dγ K=2∫(1/(3(1+γ^2 )−(1−γ^2 )))dγ=2∫(1/(3+3γ^2 −1+γ^2 ))dγ K=2∫(1/(2+4γ^2 ))dγ=∫(1/(1+2γ^2 ))dγ=∫(1/(1+((√2)γ)^2 ))dγ u=(√2)γ→du=(√2)dγ→dγ=((√2)/2)du ((√2)/2)∫(1/(1+u^2 ))du=((√2)/2)arctg(u)+cte=((√2)/2)arctg((√2)γ)+cte K=((√2)/2)arctg((√2)tan((t/2)))=((√2)/2)arctg((√2)tan(x)) K=∫(1/(1+sin^2 x))dx=((√2)/2)arctg((√2)tanx)

$${sin}^{\mathrm{2}} {x}=\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}} \\ $$$${K}=\int\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}}=\int\frac{\mathrm{1}}{\frac{\mathrm{2}+\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}}{dx} \\ $$$${K}=\int\frac{\mathrm{2}}{\mathrm{3}−{cos}\left(\mathrm{2}{x}\right)}{dx}=\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{3}−{cos}\left(\mathrm{2}{x}\right)}{dx}=_{{t}=\mathrm{2}{x}} \\ $$$${K}=\int\frac{\mathrm{1}}{\mathrm{3}−{cos}\left({t}\right)}{dt} \\ $$$$\gamma={tan}\left(\frac{{t}}{\mathrm{2}}\right)\rightarrow{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\gamma^{\mathrm{2}} \right){dx} \\ $$$${cost}=\frac{\mathrm{1}−\gamma^{\mathrm{2}} }{\mathrm{1}+\gamma^{\mathrm{2}} } \\ $$$${K}=\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{3}−\frac{\mathrm{1}−\gamma^{\mathrm{2}} }{\mathrm{1}+\gamma^{\mathrm{2}} }}×\frac{\mathrm{1}}{\mathrm{1}+\gamma^{\mathrm{2}} }{d}\gamma \\ $$$${K}=\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+\gamma^{\mathrm{2}} \right)−\left(\mathrm{1}−\gamma^{\mathrm{2}} \right)}{d}\gamma=\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{3}+\mathrm{3}\gamma^{\mathrm{2}} −\mathrm{1}+\gamma^{\mathrm{2}} }{d}\gamma \\ $$$${K}=\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{2}+\mathrm{4}\gamma^{\mathrm{2}} }{d}\gamma=\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}\gamma^{\mathrm{2}} }{d}\gamma=\int\frac{\mathrm{1}}{\mathrm{1}+\left(\sqrt{\mathrm{2}}\gamma\right)^{\mathrm{2}} }{d}\gamma \\ $$$${u}=\sqrt{\mathrm{2}}\gamma\rightarrow{du}=\sqrt{\mathrm{2}}{d}\gamma\rightarrow{d}\gamma=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{du} \\ $$$$\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{arctg}\left({u}\right)+{cte}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{arctg}\left(\sqrt{\mathrm{2}}\gamma\right)+{cte} \\ $$$${K}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{arctg}\left(\sqrt{\mathrm{2}}{tan}\left(\frac{{t}}{\mathrm{2}}\right)\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{arctg}\left(\sqrt{\mathrm{2}}{tan}\left({x}\right)\right) \\ $$$${K}=\int\frac{\mathrm{1}}{\mathrm{1}+{sin}^{\mathrm{2}} {x}}{dx}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{arctg}\left(\sqrt{\mathrm{2}}{tanx}\right) \\ $$

Commented by puissant last updated on 06/Aug/21

propre merci..

$$\mathrm{propre}\:\mathrm{merci}.. \\ $$

Answered by Olaf_Thorendsen last updated on 06/Aug/21

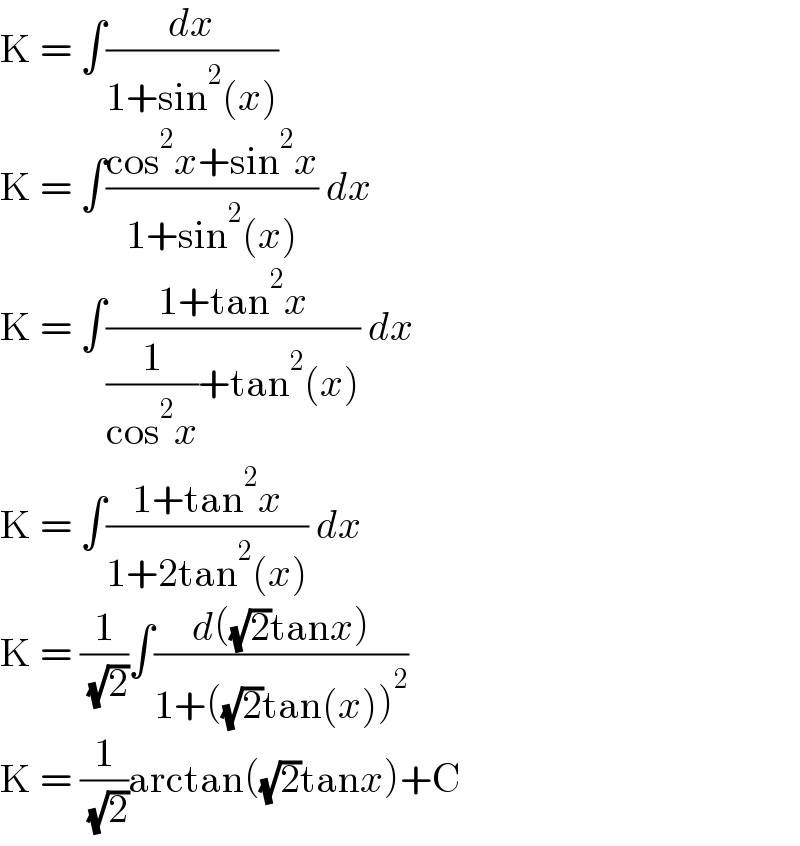
K = ∫(dx/(1+sin^2 (x))) K = ∫((cos^2 x+sin^2 x)/(1+sin^2 (x))) dx K = ∫((1+tan^2 x)/((1/(cos^2 x))+tan^2 (x))) dx K = ∫((1+tan^2 x)/(1+2tan^2 (x))) dx K = (1/( (√2)))∫((d((√2)tanx))/(1+((√2)tan(x))^2 )) K = (1/( (√2)))arctan((√2)tanx)+C

$$\mathrm{K}\:=\:\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left({x}\right)} \\ $$$$\mathrm{K}\:=\:\int\frac{\mathrm{cos}^{\mathrm{2}} {x}+\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left({x}\right)}\:{dx} \\ $$$$\mathrm{K}\:=\:\int\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} {x}}+\mathrm{tan}^{\mathrm{2}} \left({x}\right)}\:{dx} \\ $$$$\mathrm{K}\:=\:\int\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{2tan}^{\mathrm{2}} \left({x}\right)}\:{dx} \\ $$$$\mathrm{K}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{{d}\left(\sqrt{\mathrm{2}}\mathrm{tan}{x}\right)}{\mathrm{1}+\left(\sqrt{\mathrm{2}}\mathrm{tan}\left({x}\right)\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{K}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\sqrt{\mathrm{2}}\mathrm{tan}{x}\right)+\mathrm{C} \\ $$

Commented by puissant last updated on 06/Aug/21

jolie merci..

$$\mathrm{jolie}\:\mathrm{merci}.. \\ $$

Answered by nimnim last updated on 16/Aug/21

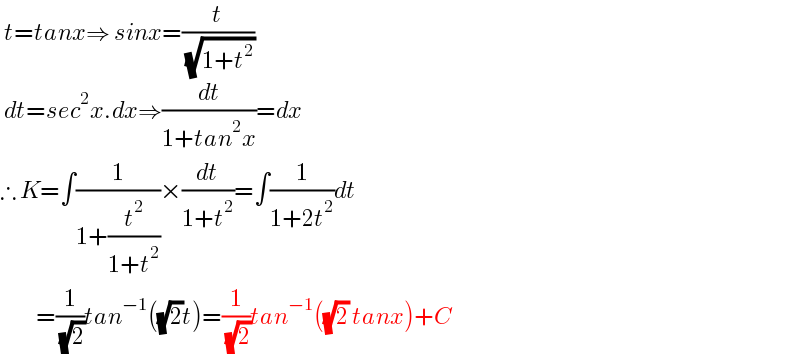
t=tanx⇒ sinx=(t/( (√(1+t^2 )))) dt=sec^2 x.dx⇒(dt/(1+tan^2 x))=dx ∴ K=∫(1/(1+(t^2 /(1+t^2 ))))×(dt/(1+t^2 ))=∫(1/(1+2t^2 ))dt =(1/( (√2)))tan^(−1) ((√2)t)=(1/( (√2)))tan^(−1) ((√2) tanx)+C

$$\:{t}={tanx}\Rightarrow\:{sinx}=\frac{{t}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\:{dt}={sec}^{\mathrm{2}} {x}.{dx}\Rightarrow\frac{{dt}}{\mathrm{1}+{tan}^{\mathrm{2}} {x}}={dx} \\ $$$$\therefore\:{K}=\int\frac{\mathrm{1}}{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }=\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{t}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}\:{tanx}\right)+{C} \\ $$

Commented by puissant last updated on 06/Aug/21

jolie..

$$\mathrm{jolie}.. \\ $$

Answered by Ar Brandon last updated on 06/Aug/21

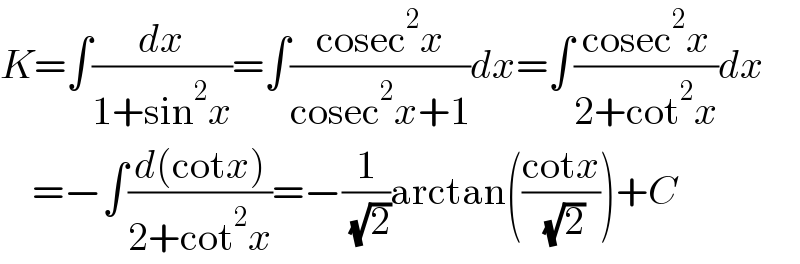
K=∫(dx/(1+sin^2 x))=∫((cosec^2 x)/(cosec^2 x+1))dx=∫((cosec^2 x)/(2+cot^2 x))dx =−∫((d(cotx))/(2+cot^2 x))=−(1/( (√2)))arctan(((cotx)/( (√2))))+C

$${K}=\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} {x}}=\int\frac{\mathrm{cosec}^{\mathrm{2}} {x}}{\mathrm{cosec}^{\mathrm{2}} {x}+\mathrm{1}}{dx}=\int\frac{\mathrm{cosec}^{\mathrm{2}} {x}}{\mathrm{2}+\mathrm{cot}^{\mathrm{2}} {x}}{dx} \\ $$$$\:\:\:\:=−\int\frac{{d}\left(\mathrm{cot}{x}\right)}{\mathrm{2}+\mathrm{cot}^{\mathrm{2}} {x}}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{cot}{x}}{\:\sqrt{\mathrm{2}}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com