Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 149667 by mnjuly1970 last updated on 06/Aug/21

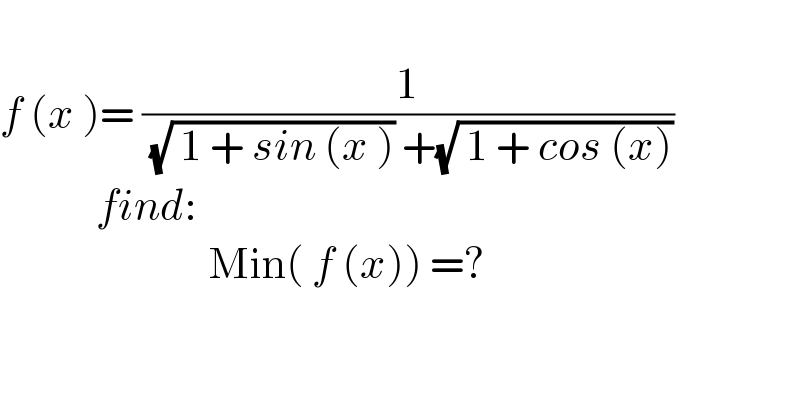
f (x )= (1/( (√( 1 + sin (x ))) +(√( 1 + cos (x))))) find: Min( f (x)) =?

$$\: \\ $$$${f}\:\left({x}\:\right)=\:\frac{\mathrm{1}}{\:\sqrt{\:\mathrm{1}\:+\:{sin}\:\left({x}\:\right)}\:+\sqrt{\:\mathrm{1}\:+\:{cos}\:\left({x}\right)}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{find}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{Min}\left(\:{f}\:\left({x}\right)\right)\:=? \\ $$$$ \\ $$

Answered by iloveisrael last updated on 07/Aug/21

f(x)=(1/(∣cos (1/2)x+sin (1/2)x∣+(√2) ∣cos (1/2)x∣)) f(x)=(1/( (√2) ∣sin ((1/2)x+(π/4))∣+(√2) ∣cos (1/2)x∣)) when cos (1/2)x =1 or (1/2)x= 0 f_1 = (1/( (√2) sin ((π/4))+(√2))) = (1/( (√2) +1))=(√2)−1 when sin ((1/2)x+(π/4))=1 or (1/2)x=(π/4) f_2 = (1/( (√2) +(√2)((1/( (√2))))))=(1/( (√2)+1))=(√2)−1 f(x)= (√2) −1 when (1/2)x=(π/8) we get f_3 =(1/( (√2) {∣sin ((3π)/8)∣+∣cos (π/8)∣})) sin ((3π)/8)=(√((1−cos ((3π)/4))/2))=(√((1+((√2)/2))/2))=(√((2+(√2))/4))=((√(2+(√2)))/2) cos (π/8)=(√((1+cos (π/4))/2))=(√((2+(√2))/4))=((√(2+(√2)))/2) f(x)_(min) =f_3 =(1/( (√2) {((√(2+(√2)))/2)+((√(2+(√2)))/2)})) = (1/( (√2) ((√(2+(√2))))))

$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mid\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\mid+\sqrt{\mathrm{2}}\:\mid\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\mid} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\mid\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)\mid+\sqrt{\mathrm{2}}\:\mid\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\mid} \\ $$$$\mathrm{when}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\:=\mathrm{1} \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}=\:\mathrm{0} \\ $$$$\mathrm{f}_{\mathrm{1}} =\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}\right)+\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{when}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}+\frac{\pi}{\mathrm{4}}\right)=\mathrm{1} \\ $$$$\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}=\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{f}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}=\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\:\sqrt{\mathrm{2}}\:−\mathrm{1} \\ $$$$\mathrm{when}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}=\frac{\pi}{\mathrm{8}}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{f}_{\mathrm{3}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\left\{\mid\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{8}}\mid+\mid\mathrm{cos}\:\frac{\pi}{\mathrm{8}}\mid\right\}} \\ $$$$\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{4}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{8}}=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{4}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)_{\mathrm{min}} =\mathrm{f}_{\mathrm{3}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\left\{\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}\right\}} \\ $$$$\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\right)} \\ $$

Commented by mnjuly1970 last updated on 06/Aug/21

thx master...

$${thx}\:{master}... \\ $$

Commented by mnjuly1970 last updated on 06/Aug/21

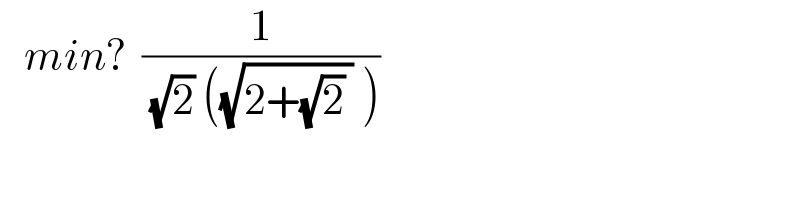
min? (1/( (√2) ((√(2+(√2) )) )))

$$\:\:\:{min}?\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}\:}\:\right)} \\ $$

Answered by EDWIN88 last updated on 07/Aug/21

f(x)=(1/( (√(1+sin x))+(√(1+cos x)))) let g(x)=(√(1+sin x)) +(√(1+cos x)) then f(x)=(1/(g(x))) , f(x)_(min) it must be g(x)_(max) ⇒take g′(x)=((cos x)/(2(√(1+sin x))))−((sin x)/(2(√(1+cos x)))) =0 ⇒cos x(√(1+cos x)) = sin x(√(1+sin x)) ⇒cos^2 x+cos^3 x=sin^2 x+sin^3 x ⇒cos^2 x−sin^2 x=sin^3 x−cos^3 x ⇒(cos x−sin x)(cos x+sin x)=−(cos x−sin x)(1+sin xcos x) ⇒(cos x−sin x){cos x+sin x+1+sin xcos x)=0 when cos x=sin x ⇒x=(π/4) g(x)_(max) = (√(1+sin (π/4)))+(√(1+cos (π/4))) g(x)_(max) =(√((2+(√2))/2))+(√((2+(√2))/2)) g(x)_(max) =2(√((2+(√2))/2)) = (√2) ((√(2+(√2)))) therefore f(x)_(min) =(1/( (√2)((√(2+(√2))))))

$${f}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}+\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}\: \\ $$$$\mathrm{let}\:{g}\left({x}\right)=\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}\:+\sqrt{\mathrm{1}+\mathrm{cos}\:{x}} \\ $$$${then}\:{f}\left({x}\right)=\frac{\mathrm{1}}{{g}\left({x}\right)}\:,\:{f}\left({x}\right)_{{min}} \:{it} \\ $$$${must}\:{be}\:{g}\left({x}\right)_{{max}} \\ $$$$\Rightarrow{take}\:{g}'\left({x}\right)=\frac{\mathrm{cos}\:{x}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}−\frac{\mathrm{sin}\:{x}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}\:=\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}\:=\:\mathrm{sin}\:{x}\sqrt{\mathrm{1}+\mathrm{sin}\:{x}} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{3}} {x}=\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{3}} {x} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}=\mathrm{sin}\:^{\mathrm{3}} {x}−\mathrm{cos}\:^{\mathrm{3}} {x} \\ $$$$\Rightarrow\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)=−\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:{x}\mathrm{cos}\:{x}\right) \\ $$$$\Rightarrow\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left\{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+\mathrm{1}+\mathrm{sin}\:{x}\mathrm{cos}\:{x}\right)=\mathrm{0} \\ $$$${when}\:\mathrm{cos}\:{x}=\mathrm{sin}\:{x}\:\Rightarrow{x}=\frac{\pi}{\mathrm{4}} \\ $$$${g}\left({x}\right)_{{max}} =\:\sqrt{\mathrm{1}+\mathrm{sin}\:\frac{\pi}{\mathrm{4}}}+\sqrt{\mathrm{1}+\mathrm{cos}\:\frac{\pi}{\mathrm{4}}} \\ $$$${g}\left({x}\right)_{{max}} =\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}} \\ $$$${g}\left({x}\right)_{{max}} =\mathrm{2}\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\:\sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\right) \\ $$$${therefore}\:{f}\left({x}\right)_{{min}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com