Question Number 1497 by Rasheed Soomro last updated on 14/Aug/15

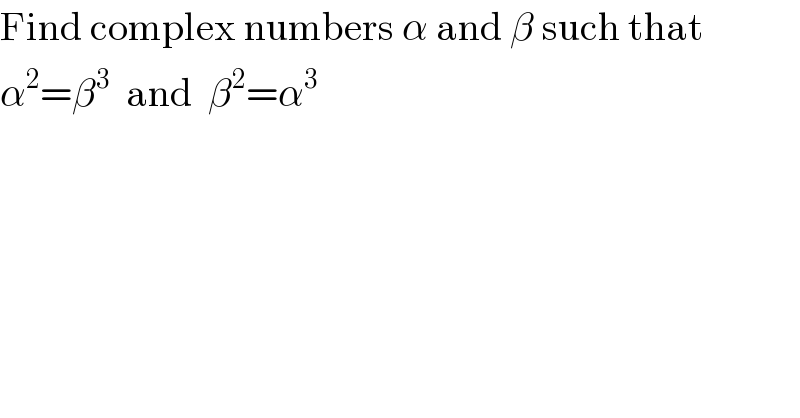
Find complex numbers α and β such that α^2 =β^3 and β^2 =α^3

Commented by123456 last updated on 14/Aug/15

(α,β)=(0,0) is ome of these pairs

Commented byRasheed Ahmad last updated on 14/Aug/15

(1,1) is an other pair.

Commented by123456 last updated on 15/Aug/15

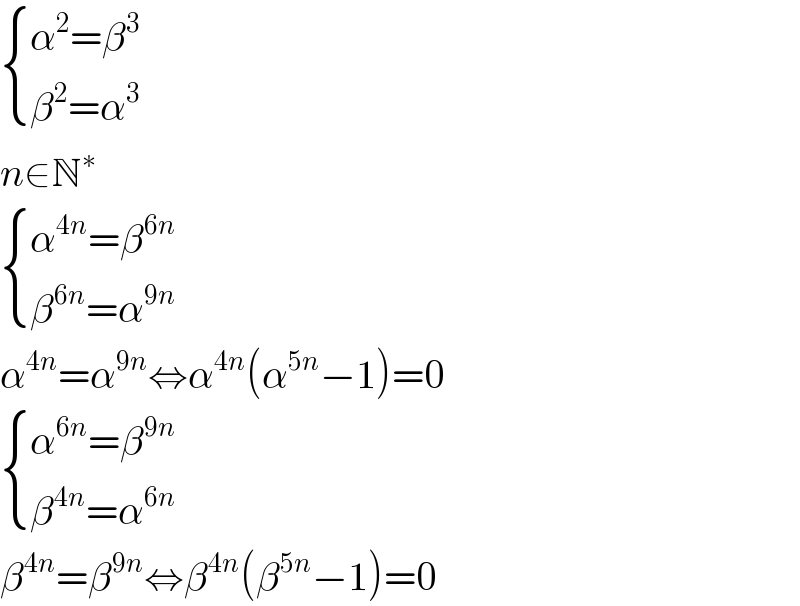
{ ((α^2 =β^3 )),((β^2 =α^3 )) :} n∈N^∗ { ((α^(4n) =β^(6n) )),((β^(6n) =α^(9n) )) :} α^(4n) =α^(9n) ⇔α^(4n) (α^(5n) −1)=0 { ((α^(6n) =β^(9n) )),((β^(4n) =α^(6n) )) :} β^(4n) =β^(9n) ⇔β^(4n) (β^(5n) −1)=0

Commented byRasheed Soomro last updated on 16/Aug/15

α^2 =β^3 (α^2 )^2 =(β^( 3) )^2 α^4 =(β^( 2) )^3 α^4 =(α^3 )^3 [substituting β^( 2) =α^3 ] α^4 =α^9 Assuming α≠0,dividing by α^4 α^5 =1⇒α=^5 (√1) Similarily , β^( 5) =1⇒β=^5 (√1) ∴ α and β both are 5th roots of unity. We know that nth root of unity=(cos((2π)/n)+ı sin((2π)/n) )^k , k=0,1,2,...(n−1) 5th root of unity=(cos((2π)/5)+ı sin((2π)/5) )^k , k=0,1,2,...4 Let cos((2π)/5)+ı sin((2π)/5) =ω 5th root of unity=1,ω,ω^2 ,ω^3 ,ω^4 (in order) Square of ∽ =1,ω^2 ,ω^4 ,ω,ω^3 (in order) Cube of ∽ =1,w^3 ,ω,ω^4 ,ω^2 (in order) (𝛚^k_1 )^2 = (𝛚^k_2 )^3 k_1 , k_2 = 0,1,2,3,4 𝛚^(2k_1 (mod 5)) =𝛚^(3k_2 (mod 5)) For 2k_1 (mod 5)=3k_2 (mod 5) : (α,β)=(ω^k_1 , ω^k_2 )=(ω^k_2 , ω^k_1 ) (α,β)={(1,1),(ω,ω^4 ),(ω^4 ,ω),(ω^2 ,ω^3 ),(ω^3 ,ω^2 )}

Commented by123456 last updated on 15/Aug/15

good approach :)

Commented byRasheed Soomro last updated on 16/Aug/15

Thanks. Please comment, although in negative , on my answers to Q−1448 and Q−1466. If the comments be positive I will gain confidence and if they are negative I will learn something. So please.....

Answered by 123456 last updated on 15/Aug/15

{ ((α^2 =β^3 )),((β^2 =α^3 )) :}⇒ { ((α^4 =β^6 )),((β^6 =α^9 )) :} α^4 =α^9 α^9 −α^4 =0 α^4 (α^5 −1)=0 α=0∨α=(1)^(1/5) α=0⇒ { ((β^3 =0)),((β^2 =0)) :}⇒β=0 α=1⇒ { ((β^3 =1)),((β^2 =1)) :}⇒ { ((β=1∨β=−(1/2)+((√3)/2)ı∨β=−(1/2)−((√3)/2)ı)),((β=1∨β=−1)) :}⇒β=1 α=e^(72°ı) ⇒ { ((β^3 =e^(144°ı) )),((β^2 =e^(216°ı) )) :}⇒ { ((β=e^(48°ı) ∨β=e^(168°ı) ∨β=e^(288°ı) )),((β=e^(108°ı) ∨β=e^(288°ı) )) :}⇒β=e^(288°ı) α=e^(144°ı) ⇒ { ((β^3 =e^(288°ı) )),((β^2 =e^(72°ı) )) :}⇒ { ((β=e^(96°ı) ∨β=e^(216°ı) ∨β=e^(336°ı) )),((β=e^(36°ı) ∨β=e^(216°ı) )) :}⇒β=e^(216°ı) α=e^(216°ı) ⇒ { ((β^3 =e^(72°ı) )),((β^2 =e^(288°ı) )) :}⇒ { ((β=e^(24°ı) ∨β=e^(144°ı) ∨β=e^(264°ı) )),((β=e^(144°ı) ∨β=e^(324°ı) )) :} α=e^(288°ı) ⇒ { ((β^3 =e^(216°ı) )),((β^2 =e^(144°ı) )) :}⇒ { ((β=e^(72°ı) ∨β=e^(192°ı) ∨β=e^(312°ı) )),((β=e^(72°ı) ∨β=e^(252°ı) )) :}⇒β=e^(72°ı) S={(0,0),(1,1),(e^(72°ı) ,e^(288°ı) ),(e^(144°ı) ,e^(216°ı) ),(e^(216°ı) ,e^(144°ı) ),(e^(288°ı) ,e^(72°ı) )}

Commented byRasheed Ahmad last updated on 15/Aug/15

(Rasheed Soomro) Excellent Sir!

Commented by123456 last updated on 15/Aug/15

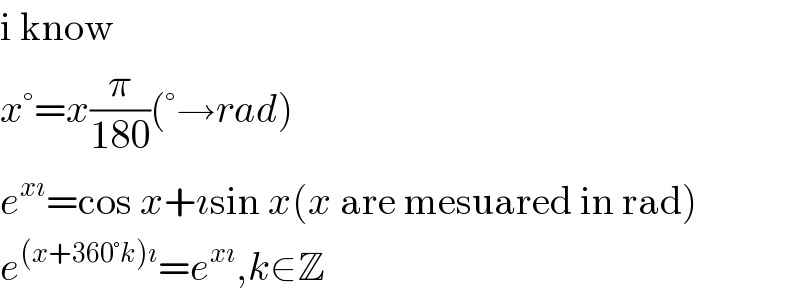
i know x°=x(π/(180))(°→rad) e^(xı) =cos x+ısin x(x are mesuared in rad) e^((x+360°k)ı) =e^(xı) ,k∈Z