Question Number 149766 by mathdanisur last updated on 07/Aug/21

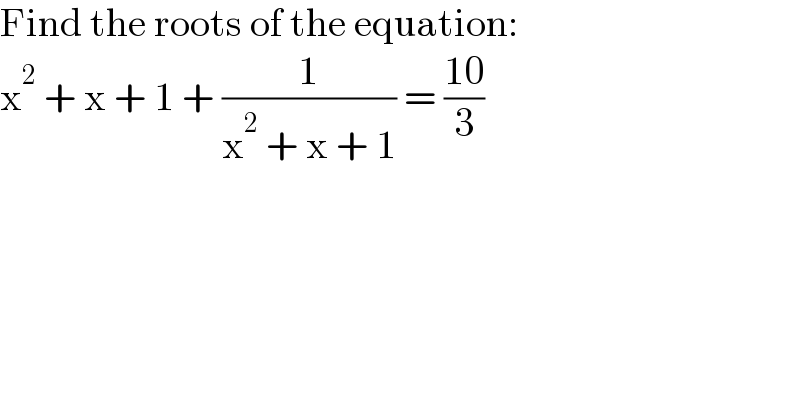
Find the roots of the equation: x^2 + x + 1 + (1/(x^2 + x + 1)) = ((10)/3)

Commented byamin96 last updated on 07/Aug/21

x^2 +x+1=y ⇒ y+(1/y)=((10)/3) y^2 +1=((10y)/3) ⇒ 3y^2 −10y+3=0 Δ=100−36=64 y=((10+8)/6)=3 x^2 +x+1=3 ⇒ x^2 +x−2=0 Δ=9 { ((x_1 =((−1+3)/2)=1)),((x_2 =((−1−3)/2)=−2)) :}

Commented bymathdanisur last updated on 07/Aug/21

Thankyou Ser

Answered by Canebulok last updated on 07/Aug/21

Solution: let: ⇒ x^2 +x+1 = k ∵ ⇒ k+(1/k) = ((10)/3) ⇒ k^2 +1 = ((10)/3)∙k ⇒ k^2 −((10)/3)∙k+1 = 0 By using quadratic formula: ⇒ k = (((((10)/3))±(√((−((10)/3))^2 −4)))/2) = (((((10)/3))±(√((64)/9)))/2) ∵ ⇒ k = 3 ; k = (1/3) By substituting back: (1st solutions) ⇒ x^2 +x+1 = 3 ⇒ x^2 +x−2 = 0 ⇒ (x+2)(x−1) = 0 ⇒ x_1 = −2 ; x_2 = 1 (2nd solutions) ⇒ x^2 +x+1 = (1/3) ⇒ x^2 +x+(2/3) = 0 By quadratic formula: ⇒ x = ((−1±(√(1^2 −4((2/3)))))/2) x_(3,4) = ((−1±i(√(5/3)))/2) Solution by: Kevin

Commented bymathdanisur last updated on 07/Aug/21

Thankyou Ser